What is perpendicular axis theorem?
लंबवत अक्ष प्रमेय क्या होता है?
लंबवत अक्ष प्रमेय ( Perpendicular Axis Theorem ) यह प्रकट करता है की –
किसी पटल ( lamina ) के तल के लंबवत अक्ष पर वस्तु का जड़त्व आघूर्ण, उस पटल के तल पर स्थित दो अन्य अक्षों पर के जड़त्व आघुर्णों के योग के बराबर होता है।
- लंबवत अक्ष का प्रमेय ( Perpendicular Axis Theorem ) दो आयामी ( two dimensional ) वस्तुओं के लिए मान्य होता है।
चित्र में दिखाए गए एक दो आयामी वृत्ताकार डिस्क पर विचार करें। मान लें कि –
- डिस्क XY तल पर स्थित है।
- डिस्क के X अक्ष पर का जड़त्व आघूर्ण ( I_{xx} ) है।
- डिस्क के Y अक्ष पर का जड़त्व आघूर्ण ( I_{yy} ) है।
- अक्ष Z डिस्क के तल पर लंबवत है तथा X और Y अक्ष के साथ संगामी है।
तब, लंबवत अक्ष का प्रमेय ( Perpendicular Axis theorem ) के अनुसार –
I_{zz} = ( I_{xx} + I_{yy} )
इसलिए, वस्तु के तल पर लंबवत किसी अक्ष पर जड़त्व आघूर्ण, वस्तु के तल पर स्थित अन्य दो लंबवत अक्षों पर के जड़त्व आघूर्ण के योग के बराबर होता है।
Polar Moment of Inertia
ध्रुवीय जड़त्व आघूर्ण
- किसी ठोस निकाय के गुरुत्व केंद्र गुजरने वाले ZZ' अक्ष पर के द्रब्यमान जड़त्व आघूर्ण ( mass moment of inertia ) को ध्रुवीय जड़त्व आघूर्ण ( Polar Moment of Inertia ) कहा जाता है।
इसे निम्न प्रकार से परिभाषित किया जाता है –
ध्रुवीय जड़त्व आघूर्ण किसी वस्तु का द्रव्यमान जड़त्व आघूर्ण होता है जो वस्तु में मरोड़ या विरूपण के लिए प्रतिरोध प्रदान करता है।
- यदि वस्तु के तल पर स्थित और गुरुत्व केंद्र ( centre of gravity ) से गुजरने वाले दो अक्षों पर का जड़त्व आघूर्ण ज्ञात हो तो लंबवत अक्ष प्रमेय द्वारा ध्रुवीय जड़त्व आघूर्ण प्राप्त किया जा सकता है।
मान लें कि कोई खंड XY तल पर स्थित है।
- तल पर स्थित XX' और YY' अक्षों पर का जड़त्व आघूर्ण ( I_{xx} ) और ( I_{yy} ) हैं।
- यदि ZZ' अक्ष पर का जड़त्व आघूर्ण ( I_{zz} ) है तब –
ध्रुवीय जड़त्व आघूर्ण \quad I_{zz} = ( I_{xx} + I_{yy} )
MOI of a uniform Rod
एक समान छड़ का जड़त्व आघूर्ण
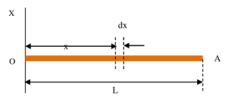
चित्र में दिखाए गए ( l ) लम्बाई और ( M ) द्रब्यमान वाले एक समान पतली छड़ OA पर विचार करें।
- छड़ का प्रति इकाई लम्बाई का द्रब्यमान \left ( \frac {M}{l} \right ) होगा।
छड़ के O शिरे से ( x ) दूरी पर स्थित ( dx ) लम्बाई के एक तत्व PQ पर विचार करें।
- तत्व का द्रव्यमान \quad dm = \left ( \frac {M}{l} \right ) dx होगा।
छड़ के लंबवत एक रेखा OX पर इस तत्व का जड़त्व आघूर्ण होगा –
dI = dm \times x^2
या, \quad dI = \left ( \frac {M}{l} \right ) dx \ x^2
- इसलिए इंटीग्रेशन विधी द्वारा OX रेखा पर सम्पूर्ण छड़ का आघूर्ण होगा –
101302 MOMENT OF INERTIA OF A ROD
I_{zz} = \int dI
= \int\limits_{0}^{l} \left ( \frac {M}{l} \right ) dx \ x^2
= \left ( \frac {M}{l} \right ) \left [ \frac {l^3}{3} \right ]_{0}^{l}
= \left ( \frac {Ml^2}{3} \right )
इस प्रकार किसी एक समान छड़ के एक शिरे से गुजरने वाली लम्बवत रेखा पर छड़ का जड़त्व आघूर्ण [ I_{zz}= \left ( \frac {Ml^2}{3} \right ) ] होता है।
MOI of a thin circular Ring
पतले वृत्ताकार वलय का जड़त्व आघूर्ण
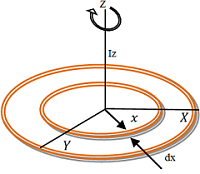
चित्र में दिखाए गए ( R ) त्रिज्या और ( M ) द्रब्यमान वाले एक पतली वलय पर विचार करें।
- वलय की कुल लम्बाई ( 2 \pi R ) होगी।
इसलिए प्रति इकाई लम्बाई का द्रब्यमान होगा –
\left ( \frac {M}{2 \pi R} \right )
वलय के ( dx ) लम्बाई वाले एक छोटे तत्व PQ पर विचार करें।
- इस तत्व का द्रब्यमान होगा –
dm = \left ( \frac {M}{2 \pi R} \right ) dx
इसलिए ZZ अक्ष पर तत्व का जड़त्व आघूर्ण होगा –
dI = dm \times R^2
= \left ( \frac {M}{2 \pi R} \right ) dx \ R^2
= \left ( \frac {MR}{2 \pi} \right ) dx
अब इंटीग्रेशन विधी द्वारा कुल वलय का जड़त्व आघूर्ण होगा –
I_{zz} = \int dI
= \int\limits_{0}^{2 \pi R} \left ( \frac {MR}{2 \pi} \right ) dx
= \left ( \frac {MR}{2 \pi} \right ) \int\limits_{0}^{2 \pi R} dx
= \left ( \frac {MR}{2 \pi} \right ) \left [ x \right ]_{0}^{2 \pi R}
= \left ( \frac {MR}{2 \pi} \right ) \left [ 2 \pi R - 0 \right ]
इसलिए, \quad I_{zz} = \left ( MR^2 \right )
इस प्रकार से किसी एक समान पतले वृत्ताकार वलय का, केंद्र से गुजरने वाले तथा वलय के तल के लम्बवत किसी अक्ष पर का जड़त्व आघूर्ण [ I_{zz} = \left ( MR^2 \right ) ] होता है।
MOI of a circular Disc
वृत्ताकार डिस्क का जड़त्व आघूर्ण
चित्र में दिखाए गए ( R ) त्रिज्या और ( M ) द्रब्यमान वाले एक वृत्ताकार डिस्क पर विचार करें।
- डिस्क का सतही क्षेत्रफल ( \pi R^2 ) है।
101304 MOMENT OF INERTIA OF DISC
अत: डिस्क के प्रति इकाई पृष्ठीय क्षेत्रफल का द्रब्यमान \left ( \frac {M}{\pi R^2} \right ) होगा।
अब डिस्क के ( x ) त्रिज्या और ( dx ) चौड़ाई के एक सूक्ष्म वलय पर विचार करें।
- इस वलय का सतही क्षेत्रफल होगा –
( 2 \pi x \times dx ) = ( 2 \pi x \ dx )
- इस वलय का द्रब्यमान होगा –
dm = \left ( \frac {M}{ \pi R^2} \right ) 2 \pi x \ dx
= \left ( \frac {2 M x }{R^2} \right ) dx
- अक्ष ZZ' पर इस वलय का जड़त्व आघूर्ण होगा –
dI = dm \ x^2
= \left ( \frac {2 M x }{R^2} \right ) x^2 \ dx
= \left ( \frac {2 M }{R^2} \right ) x^3 \ dx
- तब इंटीग्रेशन विधी द्वारा सम्पूर्ण डिस्क का जड़त्व आघूर्ण होगा –
\quad I_{zz} = \int dI
= \int\limits_{0}^{R} \left ( \frac {2 M }{R^2} \right ) x^3 dx
= \left ( \frac {2M}{R^2} \right ) \int\limits_{0}^{R} x^3 dx
= \left ( \frac {2M}{R^2} \right ) \left [ \frac {x^4}{4} \right ]_{0}^{R}
= \left ( \frac {M}{2R^2} \right ) \times R^4
इसलिए \quad I_{zz} = \left ( \frac {MR^2}{2} \right )
इस प्रकार से किसी वृत्ताकार डिस्क का, केंद्र से गुजरने वाले तथा डिस्क के तल के लम्बवत किसी अक्ष पर का जड़त्व आघूर्ण \left ( \frac {MR^2}{2} \right ) होता है।
उस विषय पर आधारित संख्यात्मक प्रश्न देखें –