What is called fluid pressure?
तरल का दबाव क्या होता है?
किसी तरल के संस्पर्श में सतह पर एक बिंदु पर तरल का दबाव ( fluid pressure ) उस बिंदु के आसपास, प्रति इकाई क्षेत्र में लंबवत कार्य करने वाला द्रव बल ( liquid thrust ) होता है।
मान लें कि, किसी तरल का कुल दबाव बल ( thrust ) ( F ) है जो लंबवत रूप से ( A ) क्षेत्र की एक सपाट सतह पर कार्य करता है।
तब, तरल के दबाव ( fluid pressure ) का मान होगा –
\text {दबाव} = \frac {\text {लम्बवत बल}}{\text {सतह का क्षेत्रफल}}
या, \quad P = \left ( \frac {F}{A} \right )
- CGS प्रणाली में, तरल के दबाव ( fluid pressure ) की इकाई \text {gm-cm}^{-2} है।
- SI प्रणाली में, तरल के दबाव ( fluid pressure ) की इकाई \text {kg-m}^{-2} है।
- तरल के दबाव ( fluid pressure ) की अन्य प्रचलित इकाइयाँ \text {पास्कल ( Pa ), बार ( bar ), psi, mm or cm पारे की ऊंचाई} इत्यादि हैं।
Expression for fluid pressure
तरल के दबाव की अभिव्यक्ति
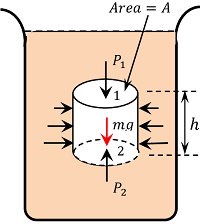
चित्र में दिखाए गए एक बीकर में रखे हुए स्थिर तरल पर विचार करें। इस तरल के एक बेलनाकार तरल निकाय ( liquid body ) पर विचार करें, जिसके अनुप्रस्थ काट का क्षेत्रफल ( A ) और ऊंचाई ( h ) है।
चूंकि, तरल का बेलनाकार निकाय संतुलन ( equilibrium ) में है, अतः पास्कल नियम ( Pascal’s law ) के अनुसार, समान गहराई पर स्थित तरल के सभी बिंदुओं पर दबाव समान होगा।
माना कि, बेलनाकार तरल निकाय के ऊपरी सतह ( 1 ) और निचली सतह ( 2 ) पर दबाव क्रमशः ( P_1 ) और ( P_2 ) है।
तरल निकाय पर ऊर्ध्वाधर दिशा में कार्य करने वाले विभिन्न बल हैं –
- ऊपरी सतह ( 1 ) पर तरल के दबाव के कारण बल ( F_1 = P_1 A ) ( यह बल नींचे कि ओर कार्य करता है। )
- निचली सतह ( 2 ) पर तरल के दबाव के कारण बल ( F_1 = P_1 A ) ( यह बल ऊपर कि ओर कार्य करता है। )
- बेलनाकार तरल निकाय का वजन ( W ) = \text {द्रब्यमान} \ \times g = \text {आयतन} \ \times \ \text {घनत्व} \ \times \ g = A h \rho g ) ( जहाँ ( \rho ) द्रव का घनत्व ( density ) है। )
चूंकि, तरल का बेलनाकार निकाय संतुलन ( equilibrium ) में है, अतः –
\text {नींचे कि ओर लगता हुआ कुल बल} = \text {ऊपर कि ओर लगता हुआ कुल बल}
अर्थात, \quad F_1 + W = F_2
या, \quad F_2 - F_1 = W
या, \quad P_2 A - P_1 A = W = A h \rho g
या, \quad ( P_2 - P_1 ) = h \rho g
Absolute pressure
पूर्ण दबाव
किसी तरल के मुक्त सतह से ( h ) की गहराई में स्थित किसी बिंदु पर के कुल दबाव को पूर्ण दबाव ( absolute pressure ) कहा जाता है।
यदि बेलनाकार तरल निकाय का ऊपरी सतह ( 1 ), तरल के मुक्त सतह से समतल होता है तब, उस सतह पर का दबाव, वायुमंडलीय दबाव ( atmospheric pressure ) के बराबर होगा –
अर्थात, \quad P_1 = P_a ( वायुमंडलीय दबाव )
मान लें कि, निचले सतह ( 2 ) पर का दबाव ( P ) है। तब –
( P ) = \text {वायुमंडलीय दबाव} + \text {तरल का दबाव}
अर्थात, \quad P = P_a + h \rho g
अतः \quad ( P - P_a ) = ( h \rho g )
इस अभिव्यक्ति से किसी भी तरल के ( h ) की गहराई पर स्थित किसी बिंदु पर के दबाव का मान ज्ञात किया जा सकता है।
Gauge pressure
गेज दबाव
किसी तरल के ( h ) गहराई पर स्थित किसी बिंदु पर के दबाव का मान ( P ) और तरल की सतह पर के दबाव का मान ( P_a ) होता है।
दबाव के इस अभिव्यक्ति \quad P = ( P_a + h \rho g ) \quad से पता चलता है कि –
P > P_a
अतः ( P - P_a ) मान के अतिरिक्त दबाव को, तरल सतह से ( h ) गहराई पर का गेज दबाव ( gauge pressure ) कहा जाता है।
अतः गेज दबाव \quad ( P - P_a ) = h \rho g
इस अभिव्यक्ति से निम्नलिखित बातों पर गौर किया जा सकता है –
- सामान गहराई या एक ही क्षैतिज तल पर स्थित सभी बिंदुओं पर तरल का दबाव सामान होता है।
- किसी बिंदु पर तरल के दबाव का मान उस बिंदु कि गहराई ( h ) पर निर्भर करता है।
- तरल के गहराई में स्थित किसी बिंदु पर कुल दबाव ( absolute pressure ) का मान ( P ) , तरल के मुक्त सतह पर के वायुमंडलीय दबाव के मान ( P_a ) से अधिक होता है। इस अतिरिक्त दबाव का मान \left ( h \rho g \right ) के बराबर होता है।
अत: द्रव में किसी एक बिंदु पर –
- दबाव किसी बर्तन के क्रॉस-सेक्शन क्षेत्र या आधार क्षेत्र पर निर्भर नहीं करता है।
- दबाव बर्तन के आकार पर निर्भर नहीं करता है।
- दबाव केवल विचाराधीन बिंदु की गहराई पर निर्भर करता है।
Pressure head
दबाव शीर्ष
तरल के मुक्त सतह से ( h ) गहराई में स्थित किसी बिंदु पर –
पूर्ण दबाव ( absolute pressure ) का मान \left ( P = P_a+ h \rho g \right ) होता है और गेज दबाव ( gauge pressure ) का मान ( P - P_a ) = h \rho g होता है।
इस अभिव्यक्ति में तरल का घनत्व ( density ) ( \rho ) , उस तरल के लिए एक स्थिरांक होता है। अतः दबाव को निम्नलिखित रूपों में परिभाषित किया जा सकता है –
- इकाई क्षेत्र पर लगते हुए एक बल के रूप में जिसकी इकाइयाँ \text {kg-cm}^2, \ \text {kg-m}^2 \ \text {or N-mm}^2, \ \text {N-m}^2 \ \text {or Pascal} ( Pa ) होती है।
- किसी अन्य तरल पदार्थ के समतुल्य स्तम्भ की ऊंचाई के रूप में जिसकी इकाइयाँ \text {mm}, \ \text {cm} \ \text {or m} हो सकती हैं।
अतः जब दबाव को किसी अन्य तरल पदार्थ के समतुल्य स्तम्भ की ऊंचाई के रूप में दर्शाया जाता है तो उसे दबाव शीर्ष ( Pressure Head ) कहते हैं।
यदि तरल की मुक्त सतह से ( h ) की गहराई पर स्थित एक बिंदु पर का गेज दबाव P हो तो –
P = h \rho g
या, दबाव शीर्ष \quad h = \left ( \frac {P}{\rho g} \right )
Pressure measurement
दबाव का मापन
किसी तरल के दबाव को मापने के लिए विभिन्न यंत्रो का प्रयोग होता है, जिनमें निम्नलिखित प्रमुख हैं –
- टोर्रिसलि बैरोमीटर। ( Torricelli’s barometer )
- बॉरडॉन दबाव मापक यन्त्र। ( Bourdon pressure gauge. )
- डायाफ्राम दबाव मापक यन्त्र। ( Diaphragm pressure gauge. )
- पीजोमीटर। ( Piezometer. )
- मैनोमीटर। ( Manometer. )
इनकी व्याख्या इस प्रकार से है –
Torricelli’s barometer
टोर्रिसलि का बैरोमीटर
एक इटालियन वैज्ञानिक ईο टोर्रिसलि ने वायुमंडलीय दबाव को सही ढंग से मापने के लिए पहली बार एक उपकरण बनाया था। इसे एक साधारण बैरोमीटर ( simple barometer ) कहा जाता है।
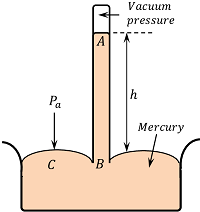
1 मीटर लंबे एक कांच की नली लेते हैं जिसका एक छोर बंद होता है। इस नली को साफ और सूखे पारे से भर दिया जाता है और खुले छोर को अंगूठे से दबाकर पारा से भरे एक बीकर में उलट दिया जाता है जैसा कि चित्र में दिखाया गया है। जब अंगूठे को हटा लिया जाता है तो नली में पारा का स्तर थोड़ा नीचे गिरकर बीकर में पारा के स्तर से ( 76 \text {cm} ) ऊपर की ऊर्ध्वाधर ( vertical ) ऊंचाई पर स्थिर हो जाता है।
नली में पारा के ऊपर का रिक्त स्थान एक परिपूर्ण वैक्यूम ( perfect vacuum ) होता है और इसे टोर्रिसलि का रिक्त स्थान ( Torricellian vacuum ) कहा जाता है।
अतः चित्र में A बिंदु पर का दबाव ( P_A = 0 ) है।
अब बीकर में पारे की सतह पर बिंदु C , और नली में समान तल पर स्थित बिंदु B पर विचार करें।
पास्कल के नियम के अनुसार –
P_B = P_C = \text {वायुमंडलीय दबाव} \ ( P_a )
यदि, नली में पारे के स्तम्भ की ऊंचाई ( h ) है और पारे का घनत्व ( density ) ( \rho ) है तब –
P_B = P_A + h \rho g
अथवा \quad P_a = 0 + h \rho g
= h \rho g
पारा वाले बैरोमीटर के लिए ( h =76 \ \text {cm} = 0.76 \ \text {m} ) पाया जाता है।
पारे का घनत्व \rho = 13.6 \times 10^3 \ \text {kg-m}^{-3} और g = 9.8 \ \text {m-s}^{-2} होता है।
अतः वायुमंडलीय दबाव का मान \quad P_a = 0.76 \times 13.6 \times 10^3 \times 9.8 = 1.013 \times 10^5 \ Pa होता है।
Bourdon’s tube pressure gauge
बॉरडॉन ट्यूब दबाव मापक यन्त्र
वायुमंडलीय दबाव से अधिक या कम के दबाव को मापने के लिए बॉरडॉन के दबाव मापक यन्त्र का उपयोग किया जाता है।
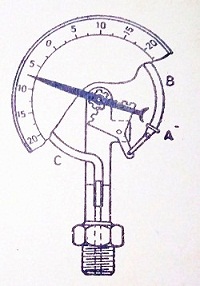
एक बॉरडॉन ट्यूब दबाव मापक यन्त्र ( Bourdon pressure gauge ), अपने सरलतम रूप में एक अण्डाकार नली ABC का बना होता है, जो वृत्त चाप ( arc ) के रूप में मुड़ा रहता है जैसा कि चित्र में दिखाया गया है। इस मुड़ा हुए ट्यूब को बॉरडॉन ट्यूब ( Bourdon tube ) कहा जाता है।
जब यंत्र के गेज ट्यूब को तरल के प्रवाह की नली से जोड़ा जाता है ( जिसका दबाव मापना होता है ), तो तरल का दबाव ट्यूब में प्रवाहित होता है। बढ़े हुए दबाव के परिणामस्वरूप बोरडॉन की नली खुद को सीधा करने का प्रयत्न करती है। चूंकि ट्यूब एक गोलाकार आवरण में युक्त होता है, इसलिए यह सीधा होने के बजाय और भी गोलकृत हो जाता है। एक छोटे पिनियन और सेक्टर व्यवस्था की मदद से बॉरडॉन ट्यूब की लोचदार विकृति ( elastic deformation ) यन्त्र के सूचक ( pointer ) को घुमाती है। यह सूचक एक अंकित पैमाने ( graduated scale ) पर चलता है, जो सीधे दबाव की मान को बताता है।
Diaphragm pressure gauge

डायाफ्राम दबाव मापक यन्त्र
वायुमंडलीय दबाव से अधिक या कम के दबाव को मापने के लिए डायाफ्राम दबाव मापक यन्त्र ( diaphragm pressure gauge ) का उपयोग किया जाता है। डायाफ्राम दबाव मापक यन्त्र में बॉरडॉन ट्यूब ( Bourdon tube ) के स्थान पर एक नालीदार डायाफ्राम ( corrugated diaphragm ) से युक्त होता है, जैसा की चित्र में दिखाया गया है।
जब यंत्र के गेज ट्यूब को तरल के प्रवाह की नली से जोड़ा जाता है ( जिसका दबाव मापना होता है ) तो तरल का दबाव, डायाफ्राम में कुछ लोचदार विकृति ( elastic deformation ) उत्पन्न करता है। एक छोटे पिनियन और सेक्टर व्यवस्था की मदद से डायाफ्राम का deformation एक सूचक को घुमाता है। यह सूचक एक अंशांकित पैमाने पर चलता है, जो सीधे दबाव की मान को बताता है।
एक डायाफ्राम दबाव नापने का यंत्र आम तौर पर अपेक्षाकृत कम दबाव को मापने के लिए उपयोग किया जाता है जबकि उच्च दबाव को मापने के लिए एक बॉरडॉन दबाव गेज का उपयोग किया जाता है।
साधारणतः एक डायाफ्राम दबाव मापक यन्त्र को कम दबाव को मापने के लिए उपयोग में लाया जाता है वहीं एक बॉरडॉन ट्यूब दबाव मापक यंत्र को अधिक दबाव को मापने के लिए उपयोग में लाया जाता है।
इस विषय पर आधारित संख्यात्मक प्रश्न देखें।
