What is called Resolution of Forces?
बलों का वियोजन क्या होता है?
बलों का वियोजन ( Resolution of forces ) का अर्थ है, किसी एक बल को दो या दो से अधिक बलों में इस प्रकार से विभाजित करना जिससे उनका संयुक्त प्रभाव दिए गए बल के समान हो।
- रिज़ॉल्यूशन की प्रक्रिया में हम किसी अज्ञात बल ( unknown force ) को हमारे हित के अनुसार दो अलग-अलग दिशाओं में विघटित करके घटक बलों में दर्शाते हैं।
- यह प्रक्रिया, बलों से संबंधित विश्लेषणात्मक समस्याओं ( numerical problems ) को हल करने में बहुत सहायक होती है।
- इस प्रकार से विभाजित बलों को घटक बल ( component forces ) कहा जाता है।
- किसी बल की रिज़ॉल्यूशन प्रक्रिया ( resolution of forces ) बलों के जोड़ प्रक्रिया ( addition of forces ) के ठीक विपरीत होती है।
- बलों का रिज़ॉल्यूशन प्रक्रिया, विश्लेषणात्मक ( analytical ) और ग्राफिकल ( graphical ) दोनों विधियों द्वारा किया जा सकता है।
Resolution into two components
दो घटक बलों में वियोजन
दिखाए गए चित्र पर विचार करें। चित्र में ( \vec R ) एक बल है जो OC रेखा पर काम कर रहा है। मान लें कि हमें इस बल OX और OY की दिशाओं में घटकों को ज्ञात करना है।
माना कि, OX और OY दिशाओं की रेखाएं OC रेखा पर क्रमशः ( \alpha ) और ( \beta ) का कोण बनाते हैं।
- रेखा OY के समांतर CA को खींचते हैं जो OX रेखा को A बिंदु पर काटती है।
- रेखा OX के समांतर CB को खींचते हैं जो OY रेखा को B बिंदु पर काटती है।
तब, रेखाखण्ड OA और OB क्रमशः OX और OY दिशाओं में बल ( \vec R ) के घटकों का प्रतिनिधित्व करेंगे।
माना कि, घटक ( OA = \vec P ) और घटक ( OB = \vec Q ) हैं।
चित्र में वेक्टर आरेख कि ज्यामिति से पता चलता है –
\angle {OCA} = \angle {BOC} ( एकान्तर कोण )।
अतः \quad \angle {OAC} = \left [ 2 \pi - \left ( \alpha + \beta \right ) \right ]
मान लें \quad \left ( \alpha + \beta \right ) = \theta
अतः \quad \angle {OAC} = \left ( 2 \pi - \theta \right )
अब, त्रिभुज ( \triangle OAC ) में साइन लॉ ( sin law ) लागू करने पर –
\left [ \frac { OA }{ \sin \beta } \right ] = \left [ \frac { AC }{ \sin \alpha } \right ] = \left [ \frac { OC }{ \sin ( 2 \pi - \theta ) } \right ]
त्रिकोणमिति अनुपातों ( trigonometrical ratios ) के अनुसार –

\sin ( 2 \pi - \theta ) = \sin \theta
अतः \left [ \frac { P }{ \sin \beta } \right ] = \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \theta \right ) } \right ]
या, \quad \left [ \frac { P }{ \sin \beta } \right ] = \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]
या, \quad \left [ \frac { P }{ \sin \beta } \right ] = \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]
पुनः \quad \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]
अतः \quad P = \left [ \frac { R \sin \beta }{ \sin \left ( \alpha + \beta \right )} \right ] \quad और \quad Q = \left [ \frac { R \sin \alpha }{ \sin \left ( \alpha + \beta \right )} \right ]
Rectangular components
आयताकार घटक
जब किसी बल को हम विश्लेषणात्मक ( analytical )या आलेख ( graphical ) विधियों द्वारा, दो परस्पर लंब दिशाओं में विघटित करते हैं तो प्राप्त घटकों को आयताकार घटक ( rectangular components ) कहा जाता है।
दिखाए गए चित्र पर विचार करें। माना कि, रेखाएं OX और OY एक दूसरे पर लंबवत हैं।
चुकीं ( \angle XOY = 90 \degree ) and ( \angle XOC = \alpha )
अतः \quad \left [ \beta = \left ( 90 \degree - \alpha \right ) \right ]
इसलिए \quad \left ( \frac{ P }{ R } \right ) = \cos \alpha

या, \quad P = R \cos \alpha ……. (1)
और \quad \left ( \frac{ Q }{ R } \right ) = \cos \beta = \cos \left ( 90 \degree - \alpha \right )
त्रिकोणमिति अनुपातों ( trigonometrical ratios ) के अनुसार –
\cos ( \pi - \alpha ) = \sin \alpha
अतः \quad \left ( \frac{ Q }{ R } \right ) = \sin \alpha
या, \quad Q = R \sin \alpha ……. (2)
जब घटक बल ( P ) और ( Q ) एक दूसरे के समकोण पर होते हैं, तो ऐसे हल किए गए घटकों को बल ( R ) के आयताकार घटक ( rectangular components ) कहे जाते हैं।
अतः समीकरण (1) और (2) से हमें पता चलता हैं कि –
- बल ( R ) से ऋणात्मक दिशा ( negative direction ) में ( \alpha ) कोण पर हल किया गया घटक बल ( P = R \cos \alpha ) होता है। इसे क्षैतिज घटक ( horizontal component ) भी कहा जाता है।
- बल ( R ) कि दिशा के घनात्मक दिशा ( positive direction ) में \left ( \beta )\right ) कोण पर हल किया गया घटक बल ( Q = R \cos \beta = R \sin \alpha ) होता है। इसे ऊर्ध्वाधर घटक ( vertical component ) भी कहा जाता है।
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –
Technique to resolve in Rectangular components
आयताकार घटक प्राप्त करने के तकनीक
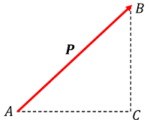
एक बल ( P ) पर विचार करें जिसे चित्र में रेखा AB के द्वारा दर्शाया गया है। इस बल को हमें AC और CB की दिशा में घटक बलों में हल करना है।
निम्नलिखित प्रक्रिया द्वारा इसका समाधान किया जाता है –
- बल ( P ) को कर्ण ( hypotenuse ) मानते हुए, एक समकोण त्रिभुज ( \triangle ABC ) का निर्माण करते हैं जैसा कि चित्र में दिखाया गया है।
- समकोण त्रिभुज के अन्य दो पक्षों को यानी आधार ( base ) और लम्ब ( perpendicular ) का प्रतिनिधित्व करने वाली रेखाएं क्रमशः AC और CB को खींचते हैं। तब, ये पक्ष घटक बलों की दिशा और परिमाण का प्रतिनिधित्व करते हैं।
- अब ज्यामिति का उपयोग कर त्रिभुज ( \triangle ABC ) के कोणों में से किसी ज्ञात कोण का पता लगते हैं।
- मान लें कि, प्रश्न में दिए गए आकड़ो और ज्यामिति कि मदद से हमें कोण ( \angle BAC = \alpha ) का मान प्राप्त हो जाता है।
ज्ञात कोण ( \angle BAC ) के संलग्न भुजा, अर्थात भुजा AC को त्रिभुज का आधार मान लेते हैं। अब त्रिकोणमिति का उपयोग कर AC और CB की दिशा में घटक बलों का निर्धारण निम्न प्रकार से करते हैं।
चुकीं \quad \cos \alpha = \left ( \frac { AC }{ AB } \right )
अतः AC = AB \ \cos \alpha = P \ \cos \alpha
इस प्रकार से AC की दिशा में घटक बल का मान होगा –
F_{AC} = P \ \cos \alpha
और CB की दिशा में घटक बल का मान होगा –
F_{CB} = P \ \sin \alpha