What is called a Spring?
स्प्रिंग क्या होता है?
स्प्रिंग ( spring ), एक यांत्रिक उपकरण होता है जिसका उपयोग ऊर्जा को संग्रहीत करने और अवश्यक्ता पड़ने पर उस ऊर्जा को निष्कासित करने के लिए किया जाता है। स्प्रिंग में संचित ऊर्जा के मान को इसका लचीलापन ( resilience ) कहते हैं।
स्प्रिंग ( spring ) दो प्रकार के होते हैं –
- पहियों के स्प्रिंग ( Leaf spring ) – ये चपटी आयताकार पत्ती के आकार के लोचदार ( elastic ) पदार्थ से बने होते हैं। इसके निर्माण में, एक या एकाधिक पत्तियों का उपयोग किया जाता है। निर्माण के समय पत्तियों पर लदाई के विपरीत दिशा में प्रारंभिक मोड़ दिया जाता है। इसे प्रारंभिक उभार ( initial camber ) कहते हैं। जब स्प्रिंग ( spring ) को लादा जाता है, तो पत्तियों पर बंकन आघूर्ण ( bending moment ) कार्य करता है। इसलिए स्प्रिंग की विशेषताएं उसके पदार्थ के यंग मापांक ( Young’s modulus ) पर निर्भर करती हैं।
- कुंडल स्प्रिंग्स ( Coil spring ) – ये कुंडली के आकर के एक लोचदार पदार्थ से बने होते हैं। जब स्प्रिंग ( spring ) को लादा जाता है, तो स्प्रिंग की कुंडलियों में एक मरोड़ ( torsion ) उत्पन्न होता है। इसलिए इस स्प्रिंग की विशेषताएं अपरूपण मापांक ( shear modulus ) पर निर्भर करती हैं।
कुंडल स्प्रिंग ( coil spring ) को पुनः दो प्रकारों में वर्गीकृत किया गया है –
- बंद कुण्डल स्प्रिंग ( Close coiled spring ) – इस प्रकार के स्प्रिंग में, हेलिक्स ( helix ) के तार के घुमावों को करीब-करीब से मोड़ा जाता है जिससे कुंडल के बीच स्थान नहीं होता है। इस स्प्रिंग्स का उपयोग होता है जहाँ खिंचाव भार ( tensile loads ) कार्य करता है। लदाई के कारण स्प्रिंग खिंचाव से लम्बा हो जाता है और भार उतारने पर अपनी सामान्य लंबाई में वापस आ जाता है।
- खुला कुण्डल स्प्रिंग ( Open coiled spring ) – इस प्रकार के स्प्रिंग में, हेलिक्स ( helix ) के तार के घुमावों को दूर-दूर से मोड़ा जाता है जिससे कुंडल के बीच स्थान होता है। इस प्रकार के स्प्रिंग ( spring ) का उपयोग होता है जहाँ संकुचनीय भार ( compressive load ) कार्य करता है। लदाई के कारण स्प्रिंग संकुचित होकर छोटा होता है और भार उतारने पर अपनी सामान्य लंबाई में वापस आ जाता है।
Use of Spring
स्प्रिंग का उपयोग
स्प्रिंग्स का उपयोग निम्नलिखित उद्देश्यों के लिए किया जाता है –
- पहियों के स्प्रिंग ( leaf spring ) का उपयोग, सड़क वाहनों जैसे कार, बस, ट्रक आदि के निलंबन प्रणाली ( suspension system ) में किया जाता है।
- कुंडली स्प्रिंग ( coiled spring ) का उपयोग, भारी वाहनों जैसे रेलवे कोच और वैगन आदि के प्राथमिक ( primary ) निलंबन प्रणाली में किया जाता है।
- स्प्रिंग का उपयोग मशीन बेड के निलंबन प्रणाली में किया जाता है जो कंपन के अधीन होते हैं।
- झटकों ( shocks ) को अवशोषित करने के लिए भिगोना ( damping ) प्रणाली में कुंडल स्प्रिंग ( coil spring ) का उपयोग किया जाता है।
- स्प्रिंग का उपयोग संपर्क सतहों के बीच बल बनाए रखने के लिए भी किया जाता है। जैसे – जनरेटर, मोटर्स आदि के कार्बन ब्रश में।
Vibration of Springs
स्प्रिंग का कंपन
इस लेख में हम कुंडल स्प्रिंग में कंपन के बारे में विस्तार से चर्चा करेंगे।
जब किसी वस्तु या द्रव्यमान ( mass ) को कुंडल स्प्रिंग के साथ लटका कर कंपन के लिए छोड़ दिया जाता है, तो वस्तु दोलन करने लगती है जो एक सरल आवर्तीय गति ( simple harmonic motions ) होता है।
Horizontal Oscillations
क्षैतिज दिशा में दोलन
चित्र में दिखाए गए, घर्षण-रहित ( friction less ) क्षैतिज मेज पर रखे एक द्रव्यमान-रहित ( mass less spring ) स्प्रिंग पर विचार करें।
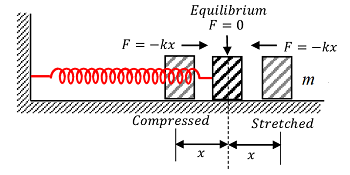
स्प्रिंग का एक सिरा एक कठोर सहारे के साथ जुड़ा होता है और दूसरा सिरा ( m ) द्रव्यमान के वस्तु से जुड़ा होता है। यदि वस्तु को थोड़ी दूरी ( x ) के लिए दाईं ओर खींचकर छोड़ दिया जाता है तो यह अपनी संतुलन की स्थिति के आगे-पीछे दोलन करना शुरू कर देता है।
वस्तु पर लगता हुआ प्रत्यावर्तन बल ( restoring force ) ( F = - k x ) होता है।
यहाँ ( k ) स्प्रिंग का बल नियतांक ( force constant ) है। ऋणात्मक चिह्न इंगित करता है कि प्रत्यावर्तन बल ( F ) , विस्थापन ( displacement ) ( x ) की दिशा के विपरीत कार्य कर रहा है।
बल की परिभाषा से –
F = m a
अतः \quad m a = - k x
इसलिए कण का त्वरण निम्न होगा –
a = - \left ( \frac { k }{ m } \right ) x
उपरोक्त समीकरण से द्रव्यमान की गति की निम्नलिखित विशेषताएं स्पस्ट होती हैं –
- यह गति स्प्रिंग की अक्ष पर आने-जाने ( to and fro ) वाली गति है।
- त्वरण ( Acceleration ), विस्थापन ( x ) का समानुपाती है। ( a \propto x ) होता हैं क्योंकि ( k ) \ \text {और} \ ( m ) स्थिरांक होते हैं।
- त्वरण, विस्थापन की दिशा के विपरीत दिशा में कार्य कर रहा है।
ये विशेषताएं एक सरल आवर्त गति ( simple harmonic motion ) के लिए आवश्यक शर्तें हैं। इसलिए, द्रव्यमान ( m ) की गति एक सरल आवर्त गति है।
इसलिए सरल आवर्तीय गति के लिए हम लिख सकते हैं –
\left ( \frac { k }{ m } \right ) = \omega ^ 2
अतः गति का आवर्त काल ( time period ) होगा –
T = \left ( \frac { 2 \pi }{ \omega } \right ) = 2 \pi \sqrt { \frac { m }{ k }}
दोलन गति की आवृत्ति ( frequency ) होगी –
\nu = \left ( \frac { 1 }{ T } \right ) = \left ( \frac { 1 }{ 2 \pi } \right ) \sqrt { \frac { k }{ m }}
Vertical Oscillations
ऊर्ध्वाधर दिशा में दोलन
चित्र में दिखाए गए, एक कठोर सहारे से ऊर्ध्वाधर रूप से लटकते हुए एक द्रव्यमान-रहित स्प्रिंग पर विचार करें जिसके दूसरे सिरे पर एक द्रव्यमान ( m ) जुड़ा हुआ है।

द्रव्यमान के भार के कारण स्प्रिंग नीचे की ओर ( d ) दूरी तक खिंच जाता है। स्प्रिंग की लोच ( elasticity ) के कारण एक प्रत्यावर्तन बल ऊपर की दिशा में कार्य करेगा।
द्रव्यमान के संतुलन के लिए –
m g = k d
यदि वस्तु को अपनी संतुलन की स्थिति से और थोड़ी दूरी ( x ) तक नींचे की ओर खींचकर छोड़ दिया जाता है तो वस्तु, प्रत्यावर्तन बल की क्रिया से अपनी संतुलन की स्थिति के “ऊपर-नीचे” ( to and fro) दोलन करना शुरू कर देता है।
इस प्रकार, वस्तु पर कार्य करने वाला परिणामी बल होगा –
F = m g - k ( d + x ) = k d - k d - k x = - k x
या, \quad F = - k x
यदि, ( a ) , वस्तु के ऊर्ध्वाधर दोलनों का रेखीय त्वरण ( linear acceleration ) है।
तब, \quad a = - \left ( \frac {k}{m} \right ) x
यह विशेषता एक सरल आवर्त गति ( simple harmonic motion ) के लिए आवश्यक शर्तें हैं। इसलिए, द्रव्यमान ( m ) की गति एक सरल आवर्त गति है।
यह स्पस्ट होता है कि, दोलनों के बल स्थिरांक ( k ) और आवर्त काल ( T ) पर, गुरुत्वाकर्षण बल ( gravitational force ) का कोई प्रभाव नहीं पड़ता है।
Parallel combination of Springs
स्प्रिंग का समानांतर संयोजन
स्प्रिंग के संयोजन में, यदि सभी स्प्रिंग का एक सिरा द्रब्यमान वस्तु से जुड़ा होता है और दूसरा सिरा सहारे से जुड़ा होता है, तो इस प्रकार के संयोजन को स्प्रिंग का समानांतर संयोजन कहा जाता है।
- चित्र (A), क्षैतिज दोलनों के लिए दो स्प्रिंगों के समानांतर संयोजन को दर्शाता है।
- चित्र (B), ऊर्ध्वाधर दोलनों के लिए दो स्प्रिंगों के समानांतर संयोजन को दर्शाता है।
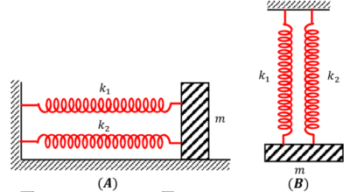
स्प्रिंग के समानांतर संयोजन में –
- अलग स्प्रिंगों के लिए बल ( F ) का मान भिन्न होता है।
- सभी स्प्रिंग की खिंचाई ( extension ) एक सामान होती है।
मान लें कि ( k _ 1 ) और ( k _ 2 ) , स्प्रिंगों के स्प्रिंग स्थिरांक ( spring constants ) हैं और प्रत्येक स्प्रिंग कि खिंचाई ( y ) है।
अत: दोनों स्प्रिंग में उत्पन्न प्रत्यावर्तन बल ( restoring force ) होगा –
( F _ 1 = k _ 1 y ) \quad और \quad ( F _ 2 = k _ 2 y )
इसलिए कुल प्रत्यावर्तन बल होगा –
F = ( F _ 1 + F _ 2 ) = - \left ( k _ 1 + k _ 2 \right ) y ……… (1)
मान लें कि, इस संयोजन का समतुल्य स्प्रिंग स्थिरांक ( equivalent spring constant ) ( k _ p ) है। तब –
F = k _ p y ………. (2)
समीकरण (1) और (2) कि तुलना से हम पाते हैं कि –
k _ p = ( k _ 1 + k _ 2 )
इसलिए, स्प्रिंग के सामानांतर संयोजन कि आवृत्ति ( frequency ) होगी –
\nu _ p = \left ( \frac { 1 }{ 2 \pi } \right ) \sqrt { \frac { k _ p }{ m }}
या, \quad \nu_p = \left ( \frac { 1 }{ 2 \pi } \right ) \sqrt { \frac { k _ 1 + k _ 2 }{ m }}
Series combination of Springs
स्प्रिंग की श्रृंखला संयोजन
स्प्रिंग के संयोजन में यदि पहले स्प्रिंग का एक सिरा सहारे से जुड़ा होता है और दूसरा सिरा दूसरे स्प्रिंग के एक छोर से जुड़ा हो, जबकि अंतिम स्प्रिंग का दूसरा सिरा दोलन करने वाली वस्तु से जुड़ा होता है और बीच के शेष सभी स्प्रिंग एक दूसरे से श्रृंखलाबद्ध जुड़े होते हैं तो इसे स्प्रिंग्स का श्रंखला संयोजन कहा जाता है।
- चित्रा (A), क्षैतिज दोलनों के लिए दो स्प्रिंग के श्रृंखला संयोजन को दर्शाता है।
- चित्र (B), ऊर्ध्वाधर दोलनों के लिए दो स्प्रिंग के श्रृंखला संयोजन को दर्शाता है।
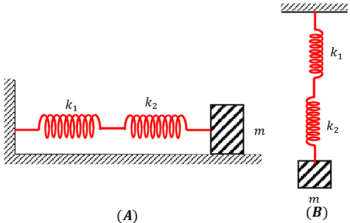
स्प्रिंग के श्रंखला संयोजन में –
- सभी स्प्रिंगों के लिए बल ( F ) का मान बराबर होता है।
- भिन्न स्प्रिंगों की खिंचाई ( extension ) भिन्न होती है।
मान लें कि ( x _ 1 ) और ( x _ 2 ) स्प्रिंगों की खिंचाई ( extension ) है।
स्प्रिंग के लिए प्रत्यावर्तन बल ( restoring force ) का मान –
F = - k _ 1 x _ 1 = - k _ 2 x _ 2
अतः \quad x _ 1 = - \left ( \frac { F }{ k _ 1} \right )
और \quad x _ 2 = - \left ( \frac { F }{ k _ 2 } \right )
स्प्रिंग समुदाय का कुल खिंचाव होगा –
x = ( x _ 1 + x _ 2 )
अतः \quad x = \left [ - \left ( \frac { F }{ k _ 1 } \right ) - \left ( \frac { F }{ k _ 2 } \right ) \right ]
= - F \left [ \left ( \frac { 1 }{ k _ 1} \right ) + \left ( \frac { 1 }{ k _ 2 } \right ) \right ] …….. (3)
मान लें कि, इस संयोजन का समतुल्य स्प्रिंग स्थिरांक ( equivalent spring constant ) ( k _ s ) है।
तब, \quad F = - k_s x
या, \quad x = - F \left ( \frac {1}{k_s} \right ) ……….. (4)
समीकरण (3) और (4) कि तुलना से हम पाते हैं कि –
\left ( \frac {1}{k _ s} \right ) = \left ( \frac {1}{k _ 1} \right ) + \left ( \frac {1}{k _ 2 } \right )
या, \quad k_s = \left ( \frac {k_1 k_2}{k_1 + k_2} \right )
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –
