What is called centre of pressure?
दबाव का केंद्र बिंदु किसे कहते हैं?
किसी तरल में निमग्न किसी सतह पर का वह बिंदु जहाँ पर परिणामी द्रवस्थैतिक बल ( hydrostatic pressure ) कार्य करता है उसे दबाव का केंद्र बिंदु ( centre of pressure ) कहा जाता है।
- ऊर्ध्वाधर या झुके हुए निमग्न सतह पर के सभी बिंदुओं पर दबाव की तीव्रता एक समान नहीं होती है।
- यह तरल के मुक्त सतह से बिंदु की गहराई ( depth ) पर निर्भर करता है।
जैसे-जैसे सतह की गहराई बढ़ती है, दबाव की तीव्रता भी बढ़ती जाती है। इसलिए, परिणामी दबाव बल एक ऐसे बिंदु पर कार्य करता है जो सतह के केन्द्रक ( centroid ) बिंदु G से कुछ नीचे स्थित होता है। इस बिंदु को दबाव का केंद्र ( centre of pressure ) कहा जाता है।
Centre of pressure of immersed surfaces
निमग्न सतह पर दबाव का केंद्र बिंदु
एक डूबे हुए सतह के किसी बिंदु पर का द्रवस्थैतिक दबाव ( hydrostatic pressure ) की तीव्रता, मुक्त तरल सतह के से उस बिंदु की गहराई पर निर्भर करती है। जैसे-जैसे बिंदु की गहराई ( \bar {h} ) बढ़ती है, दाब की तीव्रता ( p ) भी बढ़ती है।
इसलिए, द्रष्स्थैतिक दबाव की तीब्रता –
p \ \propto \bar {h}
अतः निम्नलिखित निष्कर्ष निकाले जा सकते हैं –
ऊर्ध्वाधर डूबी हुई सतह में –
( Vertical immersed surface )
सतह के केन्द्रक ( centroid ) ( G ) से गुजरने वाली एक क्षैतिज रेखा के नींचे के क्षेत्र पर दबाव की तीब्रता का औसत मान, रेखा के ऊपर के क्षेत्र पर दबाव की तीव्रता के औसत मान की तुलना में अधिक होती है।
इसलिए, ऊर्ध्वाधर डूबे हुए सतह में दबाव का केंद्र ( centre of pressure ) ( C ) हमेशा केन्द्रक ( centroid ) ( G ) के नींचे स्थित होता है।
झुके डूबे हुए सतह में –
( Inclined immersed surface )
इसी कारण से, झुके हुए सतह के केन्द्रक ( centroid ) ( G ) से गुजरने वाली एक क्षैतिज रेखा के नींचे के क्षेत्र पर दबाव की तीब्रता का औसत मान, रेखा के ऊपर के क्षेत्र पर दबाव की तीव्रता के औसत मान की तुलना में अधिक होती है।
इसलिए, झुके डूबे हुए सतह में भी दबाव केंद्र ( centre of pressure ) ( C ) हमेशा केन्द्रक ( centroid ) ( G ) के नींचे स्थित होता है।
क्षैतिज डूबे हुए सतह में –
( Horizontal immersed surface )
क्षैतिज रूप में डूबे हुए सतह का संपूर्ण क्षेत्र मुक्त पानी की सतह से समान गहराई पर स्थित होता है। इसलिए, पूरे क्षेत्र पर औसत दबाव की तीव्रता समान होती है।
इसलिए, क्षैतिज रूप से डूबे हुए सतह में दबाव केंद्र ( centre of pressure ) ( C ) , केन्द्रक ( centroid ) ( G ) के साथ मेल खाता है।
Centre of pressure of vertically immersed lamina
ऊर्ध्वाधर डूबे हुए पत्रदल का दबाव केंद्र बिंदु
एक ऊर्ध्वाधर डूबे हुए पत्रदल पर विचार करें जैसा कि चित्र में दिखाया गया है।

मान लें कि तरल की सतह से दबाव केंद्र ( centre of pressure ) की गहराई ( \bar h ) है। तरल की सतह से ( y ) गहराई पर स्थित, पत्रदल के एक मौलिक क्षेत्र ( da ) पर विचार करें।
मौलिक क्षेत्र पर कुल दबाव ( w \ y \ da ) होगा। इस बल का तरल कि सतह पर आघूर्ण ( moment ) ( w \ y^2 \ da ) होगा।
अतः पत्रदल पर लग रहे कुल दबाव ( total pressure ) का तरल कि सतह पर का आघूर्ण ( moment ) होगा –
\sum {w \ y^2 \ da} = w \sum {da \ y^2} = w \ I_0
परन्तु ( \sum {da \ y^2} ) , तरल कि सतह और पत्रदल के तल के कटाव रेखा पर का जड़त्व आघूर्ण ( moment of inertia ) को दर्शाता है। इसे ( I_0 ) से दर्शाया जाता है।
अब, पत्रदल पर का कुल दबाव –
P = w \ A \ \bar {y}
यह दबाव, पत्रदल के दबाव केंद्र ( centre of pressure ) C पर लगता है।
तरल कि सतह पर पत्रदल के ऊपर लग रहे कुल दबाव का आघूर्ण ( moment ) होगा –
P \ \bar {h} = ( w \ A \bar {y} ) \bar {h}
पत्रदल के संतुलन ( equilibrium ) के लिए –
( w \ A \bar {y} ) \bar {h} = w \ I_0
या, \quad \bar {h} = \left ( \frac {I_0}{A \bar {y}} \right )
= \left ( \frac {\text {तरल कि सतह पर क्षेत्र का द्वितीय आघूर्ण}}{\text {तरल कि सतह पर क्षेत्र का प्रथम आघूर्ण}} \right )
मान लें कि, पत्रदल के तल पर उसके केन्द्रक ( centroid ) से होकर गुजरने वाली क्षैतिज अक्ष पर, पत्रदल का जड़त्व आघूर्ण ( moment of inertia ) ( I_y ) है।
तब, सामानांतर अक्षों के प्रमेय ( parallel axes theorem ) से हम पाते हैं कि –
I_0 = I_y + A {\bar {y}}^2
अतः \quad \bar {h} = \left ( \frac {I_0}{A \bar {y}} \right ) = \left ( \frac {I_y + A {\bar {y}}^2}{A \bar {y}} \right )
= \bar {y} + \left ( \frac {I_y}{A \bar {y}} \right )
Centre of pressure of inclined immersed lamina
झुके निमग्न पत्रदल पर दबाव का केंद्र बिंदु
एक झुके हुए निमग्न पत्रदल को चित्र में दिखाया गया है।
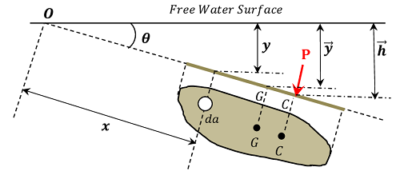
तरल के मुक्त सतह से ( y ) गहराई पर एक मौलिक क्षेत्र ( da ) पर विचार करें।
इस मौलिक क्षेत्र पर का बल होगा –
p = w \ y \ da = w \ da \ x \sin \theta
यह बल पत्रदल के ऊपर लंबवत लगता है जैसा कि चित्र में दिखाया गया है। O बिंदु पर इस बल का बल-आघूर्ण ( moment ) होगा –
( w \ da \ y ) \times x = w \ da \ x^2 \sin \theta
अतः O बिंदु पर कुल बल का बल-आघूर्ण ( moment ) होगा –
\sum w \ da \ x^2 \sin \theta = w \sin \theta \sum da \ x^2 = w \sin \theta I_0
जहाँ ( I_0 ) , तरल कि सतह और पत्रदल के तल के कटाव रेखा पर जड़त्व-आघूर्ण ( moment of inertia ) को दर्शाता है। मान लें कि C दबाव केंद्र ( centre of pressure ) है और तरल के सतह से इसकी गहराई ( \bar h ) है।
इसलिए O बिंदु से C बिंदु कि दुरी \left ( \frac {\bar h}{\sin \theta} \right ) होगी।
इसलिए, पत्रदल पर लग रहे कुल दबाव का आघूर्ण होगा –
\text {कुल दबाव} \times \frac {\bar h}{\sin \theta} = w \ A \ \bar y . \frac {\bar h}{\sin \theta}
इसलिए, \quad w \ A \ \bar y . \frac {\bar h}{\sin \theta} = w \ \sin \theta \ I_0
या, \quad \bar h = \frac {I_0}{A \ \bar y} \sin ^2 \theta
मान लें कि, तरल कि सतह के सामानांतर, पत्रदल के तल पर केन्द्रक ( centroid ) से होकर गुजरने वाली रेखा पर पत्रदल का जड़त्व आघूर्ण ( moment of inertia ) ( I_g ) है।
तरल के सतह से इस रेखा की दूरी ( \bar y \cosec \theta ) है। तब, सामानांतर अक्षों के प्रमेय ( parallel axes theorem ) से हम पाते हैं कि –
I_0 = I_g + A ( \bar y \cosec \theta )^2 = I_g + A \bar y^2 \cosec^2 \theta
इस समीकरण में ( \bar h ) का मान रखने पर –
\bar h = \left [ \frac {I_g + A \ \bar y^2 \cosec^2 \theta}{A \bar y} \right ] \sin^2 \theta
या, \quad \bar h = \bar y + \left [ \frac {I_g \sin^2 \theta}{A \bar y} \right ]
