What is Poiseuille’s formula?
पॉइसेउइले का सूत्र क्या है?
पॉइसेउइले का सूत्र ( Poiseuille’s formula ) से किसी केशिका नली ( capillary tube ) के द्वारा निष्कासित किसी शयान्तक द्रव ( viscous liquid ) के निर्वहन ( discharge ) कि मात्रा का पता चलता है। इसकी मदद से शयान्तक द्रव ( viscous liquid ) के श्यानता को ज्ञात किया जा सकता है।
मान लें कि ( l ) लम्बाई और ( r ) त्रिज्या वाले एक क्षैतिज केशिका नली ( capillary tube ) के दोनों सिरों के बीच के दबाव का अंतर ( p ) है।
तब, उस नली से प्रति सेकंड प्रवाहित होने वाले तरल कि मात्रा पॉइसेउइले का सूत्र ( Poiseuille’s formula ) से प्राप्त होता है –
Q = \frac {V}{t} = \frac {\pi \ p \ r^4}{8 \ \eta \ l}
= \frac {\pi \ p \ d^4}{128 \ \eta \ l}
इस सूत्र को श्यानता ज्ञात करने का पॉइसेउइले का सूत्र ( Poiseuille’s formula ) कहा जाता है। पॉइसेउइले का सूत्र ( Poiseuille’s formula ) की व्युत्पत्ति में मान्यताएँ हैं –
- तरल का प्रवाह स्थिर ( steady ) है और केशिका नली का अक्ष ( axis ) क्षैतिज है।
- केशिका नली के सभी बिंदुओं पर दबाव ( pressure ) स्थिर होता है।
- तरल का वेग ( velocity ) केशिका नली की दीवारों पर शून्य होता है और नली के अक्ष ( axis ) की ओर बढ़ता है।
- केशिका नली को क्षैतिज रखा जाता है ताकि गुरुत्वाकर्षण ( gravity ), तरल के प्रवाह को प्रभावित न कर सके।
Stoke’s law
स्टोक का नियम
स्टोक के नियम से किसी श्यान द्रव में गति करने वाले किसी वस्तु पर लगने वाले श्यानताक बल की अभिव्यक्ति प्राप्त होती है।
स्टोक के नियम ( Stoke’s law ) के अनुसार, श्यानताक द्रव में गति करने वाले वस्तु पर श्यानताक बल –
- वस्तु के चरम वेग ( terminal velocity ) के समानुपाती होता है, अर्थात ( F \propto v )
- वस्तु के आकार या प्रवेश क्षेत्र ( approach area ) के समानुपाती होता है, अर्थात ( F \propto r )
- तरल पदार्थ की शयानता गुणांक ( coefficient of viscosity ) के समानुपाती होता है, अर्थात ( F \propto \eta )
अतः ( r ) त्रिज्या वाली किसी गोलाकार वस्तु जब ( \eta ) श्यानता वाले एक तरल प्रदार्थ में सामान वेग ( uniform velocity ) ( v ) के साथ गमन करती है तब उस वस्तु पर शयान्तक बल ( viscous force ) होगा –
F = 6 \ \pi \ \eta \ r \ v
Stokes formula
स्टोक का समीकरण
विचार करें कि ( r ) त्रिज्या वाली एक गोलाकार वस्तु को ( \eta ) श्यानता वाले एक तरल प्रदार्थ में गिराया जाता है।
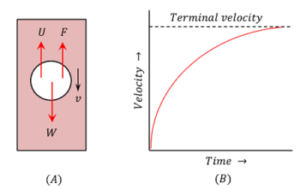
जब गोले को तरल पदार्थ में गिराया जाता है, तब समय के साथ गोले कि गति में वृद्धि होती है और कुछ समय के पश्चात वह गोला अपने अधिकतम वेग ( v ) प्राप्त करता है जो तरल प्रदार्थ की श्यानता ( viscosity ) पर निर्भर करता है। इस अवस्था में, गोले पर लगने वाले विभिन्न बलों को चित्र में दिखाया गया है। गोले पर लगने वाले विभिन्न बल हैं –
(1) गोले का वजन जो सीधा नीचे की ओर लगता है –
W = \frac {4}{3} \pi r^3 \rho g
यहाँ ( \rho ) गोले के प्रदार्थ का घनत्व ( density ) है।
(2) सीधा ऊपर की ओर लगने वाला उत्प्लावक बल ( buoyant force ) है जो विस्थापित द्रव ( displaced liquid ) के वजन के बराबर होता है।
U = \frac {4}{3} \pi r^3 \sigma g
यहाँ ( \sigma ) तरल प्रदार्थ का घनत्व ( density ) है।
(3) शयान्तक बल ( viscous force ) ( F ) जो सीधा ऊपर की दिशा में लगता हुआ बल है।
अतः वस्तु पर लगता हुआ कुल बल होगा –
F_{net} = W - ( U + F )
तब, स्टोक के नियम के अनुसार –
F = 6 \ \pi \ \eta \ r \ v
जैसे जैसे वस्तु निचे कि ओर गिरता है, गुरुत्वाकर्षण के प्रभाव से उसका वेग बढ़ता जाता है। इस प्रकार, वस्तु का वेग बढ़ने पर श्यानतक बल भी बढ़ता जाता है। एक ऐसी स्थिति पहुँचती है जब नींचे की ओर लगने वाला वस्तु का वजन, ऊपर की ओर लगने वाले श्यानतक बल और उत्प्लावकता बल के योग के बराबर हो जाता है। अर्थात ( W = U + F )
इस स्थिति में, वस्तु पर कुल बल शून्य हो जाता है और शरीर एक समान अधिकतम वेग से गिरने लगता है जिसे चरम वेग ( terminal velocity ) कहा जाता है।
जब वस्तु, चरम वेग ( terminal velocity ) ( v ) से गमन करती है, तब –
U + F = W
या, \quad \frac {4}{3} \pi r^3 \sigma g + 6 \pi \eta r v = \frac {4}{3} \pi r^3 \rho g
या, \quad 6 \pi \eta r v = \frac {4}{3} \pi r^3 ( \rho - \sigma ) g
या, \quad \eta = \frac {2 \ r^2}{9 \ v} ( \rho - \sigma )
इस अभिव्यक्ति को श्यानता ज्ञात करने का स्टोक के सूत्र के रूप में जाना जाता है।
Dashpot formula
डैशपॉट का सूत्र
डैशपॉट ( dashpot ) एक पिस्टन सिलेंडर व्यवस्था है जिसमें एक भारी शयान्तक ( viscous ) तरल का उपयोग अवमन्दक ( damping ) के उद्देश्य से किया जाता है।
मशीनों, वाहनों आदि में कंपन और झटके को कम करने के लिए डैशपॉट का उपयोग किया जाता है। डैशपॉट सिलेंडर में, सिलेंडर में एक चिपचिपा तरल या हाइड्रोलिक तेल भरा जाता है। इस तरल को डैशपॉट तेल ( dashpot oil ) कहा जाता है।
डैशपॉट तेल द्वारा लगाए गए शयान्तक बल ( viscous force ) के खिलाफ पिस्टन डैशपॉट सिलेंडर में चलता है। एक डैशपॉट ( dashpot ) पर विचार करें जिसमें –
- ( W ) बाह्य बल के साथ पिस्टन का वजन है।
- ( D ) पिस्टन का व्यास है।
- ( l ) पिस्टन की लंबाई है।
- ( t ) पिस्टन और डैशपॉट सिलेंडर के बीच का clearance है।
- ( v ) डैशपॉट में पिस्टन का चरम वेग ( terminal velocity ) है।
तब श्यानता का मान निम्नलिखित समीकरण से प्राप्त किया जा सकता है –
\eta = \frac {4 W t^3}{3 \pi D^3 l v }
