What are Simple Harmonic Motion Equations?
सरल आवर्तीय गति समीकरण क्या हैं?
वह समीकरण जो सरल आवर्तीय गति का नियंत्रण और उसके गुणों को दर्शाता है उसे सरल आवर्तीय गति समीकरण ( simple harmonic motion ) कहते हैं।
सरल आवर्तीय गति समीकरण ( SHM ) कर रहे वस्तु का समय ( t ) में माध्य बिंदु से विस्थापन को दर्शाता है।
यदि कोई कण स्थिर वृत्तीय गति ( uniform circular motion ) कर रहा होता है तो एक निश्चित व्यास पर उसका प्रक्षेपण ( projection ), एक सरल आवर्तीय गति करेगा। इसलिए, सरल आवर्तीय गति समीकरण ( simple harmonic motion equation ) को किसी कण की स्थिर वृत्तीय गति ( uniform circular motion ) के मूल सिद्धांतों से प्राप्त करना आसान हो जाता है।
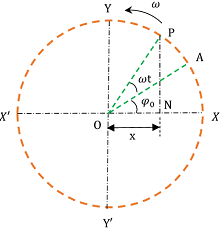
चित्र में दिखाए गए कण P पर विचार करें जो त्रिज्या ( A ) के एक वृत्त परिधि पर स्थिर कोणीय त्वरण ( angular velocity ) ( \omega ) से वामावर्त ( anti-clockwise ) दिशा में गति कर रहा है। मान लीजिए –
- ( t = 0 ) समय पर कण A बिंदु पर है और ( \angle { XOA } = \phi _{ 0 } ) है।
- ( t = t ) समय पर कण, P बिंदु पर पहुँचता है और ( \angle { AOP } = \omega t ) है।
- वृत्त के एक निश्चित व्यास XX' पर लम्ब PN को खींचा जाता है।
जब कण P वृत्त की परिधि पर चलता है तो लम्ब का पाद बिंदु N , व्यास XX' पर आने-जाने ( to and fro ) वाली गति में होता है।
इसलिए, लम्ब के पाद ( N ) की गति, एक सरल आवर्तीय गति होती है।
Displacement in Simple Harmonic Motion
सरल आवर्तीय गति में विस्थापन
माध्य बिंदु से ( t ) समय पश्चात् लम्ब के बिंदु N का विस्थापन ( displacement ) होगा –
x = ON
अब, समकोण त्रिभुज \triangle {ONP} में –
\angle { PON } = ( \omega t + \phi _ { 0 } )
अतः \quad \left ( \frac { ON }{ OP } \right ) = [ \cos ( \omega t + \phi _{ 0 } ) ]
या, \quad \left ( \frac { x }{ A } \right ) = [ \cos ( \omega t + \phi _{ 0 } ) ]
अतः \quad x = [ A \cos ( \omega t + \phi _ { 0 } ) ] …….. (1)
इस समीकरण को सरल आवर्तीय गति समीकरण ( simple harmonic motion equation ) कहते हैं।
यह समीकरण, कण के प्रारंभिक स्थिति ( initial position ) से ( t ) समय के बाद कण के विस्थापन को बताता है। पद ( \omega t + \phi _ { 0 } ) को कण का फेज़ ( phase ) कहा जाता है और ( \phi _{ 0 } ) को प्रारंभिक फेज़ ( initial phase ) या फेज़ कांस्टेंट ( phase constant ) कहा जाता है। ( A ) को गति का आयाम ( amplitude ) कहा जाता है। जब कण चरम स्थिति ( extreme position ) पर होता है तो कण का अधिकतम विस्थापन ( \pm A ) होता है।
Velocity in Simple Harmonic Motion
सरल आवर्तीय गति में वेग
एक सरल आवर्तीय गति समीकरण ( simple harmonic motion equation ) इस प्रकार है –
x = A \cos ( \omega t + \phi _ { 0 } ) ……… (1)
इस समीकरण को differentiating करने पर हम पाते हैं कि –
\left ( \frac { dx }{ dt } \right ) = - \omega A \sin ( \omega t + \phi _ { 0 } )
परन्तु, गति के किनेमेटिक समीकरण ( kinematic equations ) के अनुसार, वेग ( velocity ) –
v = \left ( \frac { dx }{ dt } \right )
अतः \quad v = - \omega A \sin ( \omega t + \phi _ { 0 } ) ……… (2)
इस समीकरण को इस तरह भी लिखा जा सकता है –
v = - \omega \sqrt { A ^ 2 \sin ^ 2 ( \omega t + \phi _ { 0 } )}

= - \omega \sqrt { A ^ 2 [ 1 - \cos ^ 2 ( \omega t + \phi _ { 0 } ) ]}
= - \omega \sqrt { [ A ^ 2 - A ^ 2 \cos ^ 2 ( \omega t + \phi _ { 0 } ) ]}
= - \omega \sqrt { ( A ^ 2 - x ^ 2 )} …….. (3)
इस समीकरण से हम पाते हैं कि – जब विस्थापन न्यूनतम होता है, तब वेग अधिकतम होगा। परन्तु विस्थापन का न्यूनतम मान शुन्य होता है।
अतः, समीकरण (3) में ( x = 0 ) मान रखने पर।
v _ { max } = \omega A
विस्थापन और वेग के बीच के सम्बन्ध को चित्र में आरेख के द्वारा दर्शाया गया है।
Acceleration in Simple Harmonic Motion
सरल आवर्तीय गति में त्वरण
सरल आवर्तीय गति में कण के वेग की अभिव्यक्ति इस प्रकार से होती है –
v = - \omega A \sin ( \omega t + \phi _ { 0 } ) …….. (2)
इस समीकरण को differentiating करने पर हम पाते हैं –
\left ( \frac { d v }{ d t } \right ) = - \omega ^2 A \cos ( \omega t + \phi _ { 0 } ) = - \omega ^ 2 x

गति के किनेमेटिक समीकरण ( kinematic equations ) के अनुसार त्वरण ( acceleration ) होता है –
a = \left ( \frac { d v }{ d t } \right )
अतः \quad a = - \omega ^ 2 x …….. (4)
यहाँ ऋणात्मक चिन्ह ( – ) यह बताता है कि त्वरण, विस्थापन के के दिशा के विपरीत होता है। समीकरण के अनुसार, जब विस्थापन अधिकतम होगा तब त्वरण भी अधिकतम होगा। परन्तु, विस्थापन का अधिकतम मान, चरम बिन्दुओं ( extreme positions ) पर ( \pm A ) के बराबर होता है।
अतः \quad a _ {max} = \omega ^ 2 A
विस्थापन और त्वरण के बीच सम्बन्ध को चित्र में आरेख के द्वारा दर्शाया गया है।
Time period
आवर्त काल
एक पूर्ण चक्र को पूरा करने में लगने वाले समय को आवर्त काल ( time period ) कहते हैं।
कण एक स्थिर कोणीय वेग ( \omega ) से एक चक्र को पूरा करने में, ( 2 \pi ) रेडियन का कोणीय विस्थापन ( angular displacement ) करता है।
अतः सरल आवर्त गति का आवर्त काल होगा –
T = \left ( \frac { 2 \pi }{ \omega } \right ) ……… (5)
= 2 \pi \left ( \frac { 1 }{ \omega } \right )
समीकरण (4) से हम पाते हैं कि –
\omega = \sqrt {\left ( \frac {a}{x} \right ) }
अतः \quad T = 2 \pi \left ( \frac { x }{ a } \right ) ………. (6)
= 2 \pi \sqrt { \frac {\text {विस्थापन}}{\text {त्वरण}}}
सरल आवर्त गति ( Simple harmonic motion ) के लिए –
( F = m a ) \quad और \quad ( F = - k x )
इसलिए, \quad \left ( \frac { x }{ a } \right ) = \left ( \frac { m }{ k } \right )
अतः \quad T = 2 \pi \sqrt { \left ( \frac { m }{ k } \right ) } ……. (7)
Frequency
आवृत्ति
प्रति इकाई समय में होने वाले दोलनों की संख्या को सरल आवर्तीय गति की आवृत्ति ( frequency ) कहा जाता है।
आवृत्ति ( frequency ), आवर्त काल ( time period ) का व्युत्क्रम ( reciprocal ) होता है।
अतः \quad \nu = \left ( \frac { 1 }{ T } \right )
इस प्रकार, समीकरण (6) से हम पाते हैं कि –
\nu = \left ( \frac { 1 }{ 2 \pi } \right ) \sqrt {\left ( \frac { a }{ x } \right )} ……… (8)
समीकरण (7) से हम पाते हैं कि –
\nu = \left ( \frac { 1 }{ 2 \pi } \right ) \sqrt {\left ( \frac { k }{ m } \right )} ……… (9)
Angular frequency
कोणीय आवृत्ति
इकाई समय में कोणीय विस्थापन को आवर्त गति ( periodic motion ) की कोणीय आवृत्ति ( angular frequency ) कहा जाता है।
इकाई समय में कोणीय विस्थापन होगा –
\nu \times 2 \pi
अतः वृत्तीय आवृत्ति ( \nu ) को ( 2 \pi ) से गुणा करने से कोणीय आवृत्ति प्राप्त होता है।
इसलिए, कोणीय आवृत्ति \quad \omega = 2 \pi \nu = \left ( \frac { 2 \pi }{ T } \right )
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –
Resoring Force
प्रत्यावर्तन बल
जब एक कण सरल आवर्तीय गति कर रहा होता है, तो उस कण पर एक बल कार्य करता है जिसमें कण को उसकी माध्य स्थिति ( mean position ) में लाने की प्रवृत्ति होती है। इस बल को प्रत्यावर्तन बल ( restoring force ) कहते हैं।
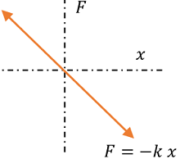
सरल आवर्तीय गति के लिए –
F = - k x
प्रत्यावर्तन बल, कण के माध्य स्थिति से विस्थापन के समानुपाती होता है।
सरल आवर्तीय गति के त्वरण के लिए –
a = - \omega ^ 2 x
अतः \quad F = m a = - m \omega ^ 2 x
या, \quad k x = m \omega ^ 2 x
अतः \quad F = - k x = - m \omega ^ 2 x
यहाँ ( k ) को बल नियतांक ( Force constant ) कहा जाता है।
अतः एक सरल आवर्तीय गति का बल नियतांक होता है –
k = m \omega ^ 2
साथ ही \quad \omega = \sqrt { \left ( \frac { k }{ m } \right ) }
विस्थापन और प्रत्यावर्तन बल के बीच सम्बन्ध को चित्र में आरेख के द्वारा दर्शाया गया है।
Forms of Simple Harmonic Motion Equations
सरल आवर्तीय गति के समीकरण के रूप
कण की प्रारंभिक स्थितियों के आधार पर, सरल आवर्तीय गति समीकरण को विभिन्न रूपों में व्यक्त किए जाता है। इन्हें निम्न चित्रों में प्रदर्शित किया गया है।
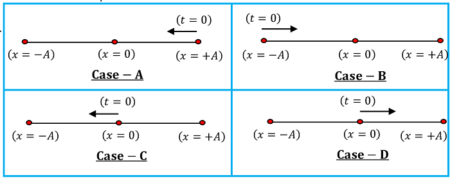
(1) स्थिति – A ( दाईं ओर की चरम स्थिति से कण ऋणात्मक ( X ) दिशा में गति करना शुरू करता है। )
चित्र संख्या Case – A पर विचार करें।
प्रारम्भ में कण दाईं ओर की चरम स्थिति ( right extreme position ) में होता है। अर्थात, ( t = 0 ) समय पर कण की स्थिति ( x = + A ) पर है। इस प्रकार कण, ऋणात्मक ( X ) दिशा में चलता है। अर्थात, स्थिति ( x = + A ) से प्रारम्भ होकर स्थिति ( x = 0 ) की दिशा में।
इस सरल आवर्तीय गति का सामान्य समीकरण इस प्रकार होगा –
x = A \cos ( \omega t + \phi _ { 0 } ) ……… (1A)
(2) स्थिति – B ( बाईं ओर की चरम स्थिति से कण घनात्मक ( X ) दिशा में गति करना शुरू करता है। )
चित्र संख्या Case – B पर विचार करें।
प्रारम्भ में कण बाईं ओर की चरम स्थिति ( left extreme position ) में होता है। अर्थात, ( t = 0 ) समय पर कण की स्थिति ( x = - A ) पर है। इस प्रकार कण, घनात्मक ( X ) दिशा में चलता है। अर्थात, स्थिति ( x = - A ) से प्रारम्भ होकर स्थिति ( x = 0 ) की दिशा में।
इस सरल आवर्तीय गति का सामान्य समीकरण इस प्रकार होगा –
x = - A \cos ( \omega t + \phi _ { 0 } ) ……… (1B)
(3) स्थिति – C ( माध्य स्थिति से कण ऋणात्मक ( X ) दिशा में गति करना शुरू करता है। )
चित्र संख्या Case – C पर विचार करें।
प्रारम्भ में कण, माध्य स्थिति ( mean position ) पर होता है। अर्थात, ( t = 0 ) समय पर कण की स्थिति ( x = 0 ) पर है। इस प्रकार कण, माध्य स्थिति से ऋणात्मक ( X ) दिशा में चलता है। अर्थात, स्थिति ( x = 0 ) से प्रारम्भ होकर स्थिति ( x = - A ) की दिशा में।
इस सरल आवर्तीय गति का सामान्य समीकरण इस प्रकार होगा –
x = - A \sin ( \omega t + \phi _ { 0 } ) ……… (1C)
(4) स्थिति – D ( माध्य स्थिति से कण घनात्मक ( X ) दिशा में गति करना शुरू करता है। )
चित्र संख्या Case – D पर विचार करें।
प्रारम्भ में कण माध्य स्थिति ( mean position ) पर होता है। अर्थात, ( t = 0 ) समय पर कण की स्थिति ( x = 0 ) पर है। इस प्रकार कण, माध्य बिंदु से घनात्मक ( X ) दिशा में चलता है। अर्थात, स्थिति ( x = 0 ) से प्रारम्भ होकर स्थिति ( x = + A ) की दिशा में।
इस सरल आवर्तीय गति का सामान्य समीकरण इस प्रकार होगा –
x = A \sin ( \omega t + \phi _ { 0 } ) ……… (1D)
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –
