What is called Centripetal Acceleration?
जब कोई कण स्थिर वृत्तीय गति ( uniform circular motion ) में होता है, तो उसकी चाल ( speed ) स्थिर रहती है परन्तु चाल की दिशा में निरंतर परिवर्तन के कारण उसका वेग ( velocity ) लगातार बदलता रहता है। इसलिए, वृत्तीय गति निरंतर त्वरित होती रहती है।
स्थिर वृत्तीय गति वाले वस्तु पर एक त्वरण ( acceleration ) द्वारा कार्य किया जाता है जो त्रिज्या के साथ वृत्ताकार पथ के केंद्र की ओर निर्देशित होता है। इस त्वरण को अभिकेन्द्रीय त्वरण ( centripetal acceleration ) कहते हैं।
Magnitude of Centripetal Acceleration
अभिकेन्द्रीय त्वरण का मान
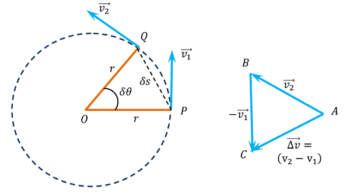
चित्र में दिखाए गए एक कण पर विचार करें जो एक स्थिर गति ( v ) के साथ ( r ) त्रिज्या के एक गोलाकार पथ में गति कर रहा है।
मान लीजिए कि ( t ) समय पर कण P बिंदु पर है और ( \delta t ) समय के बाद यह Q बिंदु पर पहुँचता है।
मान लें कि P और Q बिंदुओं पर वेग क्रमशः ( v_1 ) और ( v_2 ) हैं और वे इन बिन्दुओं पर स्पर्शरेखीय दिशा में निर्देशित होते हैं।
अब वेग का वेक्टर त्रिभुज खींचा जाता है जैसा कि चित्र में दिखाया गया है। वेक्टर त्रिभुज में –
- भुजा AB वेग वेक्टर ( v_2 ) का प्रतिनिधित्व करता है।
- भुजा BC वेग वेक्टर ( - v_1 ) का प्रतिनिधित्व करता है।
अब त्रिभुज को बंद करने के लिए वेक्टर AC को खींचा जाता है। तब वेक्टर AC , वेग में परिवर्तन अर्थात \Delta v = ( v_2 - v_1 ) का प्रतिनिधित्व करेगा।
चुकि ( \delta t ) बहुत सूक्ष्म होता है, अतः –
\text {वृत्तीय जीवा} \ PQ \ \simeq \ \text {वृत्तीय चाप} \ PQ
ऐसी स्थिति में, त्रिज्या खंड ( sector ) OPQ को एक त्रिभुज माना जा सकता है।
अब, त्रिभुज \triangle {OPQ} और \triangle {ABC} से हम पाते हैं कि –
- \angle {POQ} = \angle {ABC} = \delta \theta
- \left ( \frac {OP}{OQ} \right ) = 1 \quad ( दोनों वृत्तीय पथ कि त्रिज्या r हैं )
- \quad \left ( \frac {AB}{BC} \right ) = 1 \quad ( दोनों रैखिक वेग \omega r हैं )
अतः ( \triangle {OPQ} ) \ \text {और} \ ( \triangle {ABC} ) सर्वांगसम हैं। ( SAS के द्वारा )
इसलिए \quad \left ( \frac {AC}{PQ} \right ) = \left ( \frac {BC}{OP} \right ) = \left ( \frac {AB}{OQ} \right )
अब, \quad \left [ \left ( \frac {AC}{PQ} \right ) = \left ( \frac {AB}{OQ} \right ) \right ] का मान लेने पर –
\left ( \frac {\Delta v}{\delta s} \right ) = \left ( \frac {v}{r} \right )
या, \quad \Delta v = \left ( \frac {v}{r} \right ) \delta s
समीकरण के दोनों पक्षों को ( \delta t ) से भाग देने पर हम पाते हैं कि –
\left ( \frac {\Delta v}{\delta t} \right ) = \left ( \frac {v}{r} \right ) \left ( \frac {\delta s}{\delta t} \right )
अतः \quad \left ( \frac {dv}{dt} \right ) = \left ( \frac {v}{r} \right ) \left ( \frac {ds}{dt} \right )
परन्तु, \quad \left ( \frac {dv}{dt} \right ) = a \quad और \quad \left ( \frac {ds}{dt} \right ) = v
अतः \quad a = \left ( \frac {v}{r} \right ) v
या \quad a = \left ( \frac {v^2}{r} \right ) = \omega^2 r \quad क्योंकि \quad ( v = \omega r )
इसलिए, अभिकेन्द्रीय त्वरण का परिमाण a = \left ( \frac {v^2}{r} \right ) \quad या \quad a = \omega^2 r होता है।
Direction of Centripetal Acceleration
अभिकेन्द्रीय त्वरण की दिशा
जब कोई कण एक वक्रीय या वृत्तीय पथ पर गमन करता है उस समय अभिकेन्द्रीय त्वरण कार्य करता है। इसलिए, वृत्तीय गति निरंतर त्वरित होती रहती है। यह वह त्वरण होता है जो किसी कण को वक्रीय या वृत्तीय पथ पर गमन करते रहने के लिए आवश्यक बल प्रदान करता है।
अतः अभिकेन्द्रीय त्वरण हमेशा त्रिज्या के साथ कात्या करता है और इसकी दिशा वक्रीय या वृत्तीय पथ के केंद्र की ओर निर्देशित होती है।
उदहारण –
ऊपर दिए गए चित्र पर विचार करें। जब वस्तु ( P ) बिंदु पर है, तब अभिकेन्द्रीय त्वरण, बिंदु ( P \rightarrow O ) की दिशा में लग रहा है और हैब वस्तु ( Q ) बिंदु पर है, तब अभिकेन्द्रीय त्वरण, बिंदु ( Q \rightarrow O ) की दिशा में लग रहा है।
Centripetal Force
अभिकेंद्रीय बल
अभिकेंद्री बल, वह बल होता है जो किसी वस्तु को एक स्थिर गति से वृत्ताकार पथ पर गति करने के लिए आवश्यक होता है। यह हमेशा त्रिज्या के साथ ( along radius ) वृत्ताकार पथ के केंद्र की ओर कार्य करता है।
न्यूटन के गति के दूसरे नियम ( Newton’s second law of motion ) के अनुसार, ( m ) द्रव्यमान ( mass ) वाले एक वस्तु को त्रिज्या ( r ) के एक वृत्ताकार पथ में गति करने के लिए आवश्यक अभिकेंद्रीय बल ( centripetal force ) होता है –
F = \text {द्रब्यमान} \ \times \ \text {त्वरण}
= m \times \left ( \frac {v^2}{r} \right ) = \left ( \frac {mv^2}{r} \right )
= \left [ \frac {m \left (r \omega \right )^2}{r} \right ] = m r \omega^2
अभिकेंद्रीय बल के उदहारण हैं –
- एक पत्थर को जब एक वृत्तीय पथ में घुमाया जाता है तो डोरी का तनाव अभिकेन्द्रीय बल प्रदान करता है।
- सूर्य के चारों ओर ग्रहों की गति के लिए ग्रहों पर आवश्यक अभिकेन्द्रीय बल सूर्य द्वारा लगाए गए गुरुत्वाकर्षण बल के कारण होता है।
- जब एक कार क्षैतिज सड़क पर एक गोलाकार मोड़ लेती है तो टायर और सड़क के बीच का घर्षण बल ही अभिकेन्द्रीय बल प्रदान करता है।
- इलेक्ट्रॉन और नाभिक के बीच इलेक्ट्रोस्टैटिक बल ( electrostatic force ) इलेक्ट्रॉनों को नाभिक के चारों ओर घूमने के लिए अभिकेन्द्रीय बल प्रदान करते हैं।
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –
