What is called Hydrostatic pressure?
द्रवस्थैतिक दबाव क्या होता है?
द्रवस्थैतिकी ( Hydrostatics )विज्ञान की वह शाखा है जो स्थिरावस्था में किसी तरल पदार्थ के द्रवस्थैतिक दबाव ( hydrostatic pressure ) के अध्ययन से संबंधित होती है।
- जब एक तरल स्थिरावस्था में होता है तो वह पात्र के सभी दीवारों पर दबाव डालता है।
- इसी प्रकार जब कोई सतह किसी तरल द्रव्यमान में डूबी होती है तो वह तरल द्वारा कुछ दबाव को अनुभव करती है।
- इस दबाव की तीव्रता, तरल के मुक्त सतह से डूबे हुए सतह की गहराई पर निर्भर करती है।
Total hydrostatic pressure
कुल द्रवस्थैतिक दबाव
किसी तरल में डूबे हुए एक सतह पर तरल द्वारा पर लगाए गए कुल द्रव बल ( total thrust ) को कुल द्रवस्थैतिक दबाव ( total hydrostatic pressure ) कहा जाता है।
कुल दबाव ( P ) को निम्न अभिव्यक्ति से प्राप्त किया जाता है –
P = p_1 \ a_1 + p_2 \ a_2 + p_3 \ a_3 + ......
यहाँ p_1, \ p_2, \ p_3, ...... इत्यादि, डूबे हुए सतह के विभिन्न सूक्ष्म पट्टियों ( elemental strips ) पर दाब शीर्ष ( pressure head ) है और a_1, \ a_2, \ a_3, ...... इन पट्टियों पर का क्षेत्रफल है।
Pressure on vertically immersed lamina
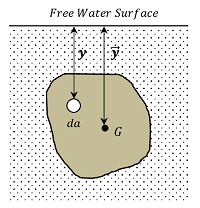
खड़े निमग्न पत्रदल पर कुल दबाव
एक खड़े पत्रदल पर विचार करें जिसका क्षेत्रफल ( A ) है जो एक तरल में ऊर्ध्वाधर डूबा हुआ है। तरल का विशिष्ट भार ( specific weight ) ( w ) है।
चित्र के अनुसार, तरल की सतह से ( y ) गहराई पर स्थित पत्रदल के एक मौलिक क्षेत्र ( da ) पर विचार करें।
इस मौलिक क्षेत्र पर दबाव की तीब्रता ( intensity of pressure ) होती है –
p = w y
इसलिए मौलिक क्षेत्र पर दबाव बल होगा –
p = w \ y \times da
इसलिए पत्रदल पर कुल दबाव बल होगा –
P = \sum {w \ y \ da} = w \sum {da \ y}
इस समीकरण में ( \sum {da \ y} ) पद, पत्रदल के क्षेत्र का तरल की मुक्त सतह पर का आघूर्ण ( moment ) है।
इसलिए \quad \sum {da \ y} = A \bar {y}
जहाँ \quad \bar {y} = , तरल की मुक्त सतह से पत्रदल के केन्द्रक ( centroid ) बिंदु की गहराई है।
Pressure on inclined immersed lamina
झुके हुए निमग्न पत्रदल पर दबाव
एक समतल पत्रदल पर विचार करें जिसका क्षेत्रफल ( A ) है और उसका सतह, तरल कि सतह से ( \theta ) का कोण पर झुका हुआ है। इसे चित्र में दिखाया गया है।
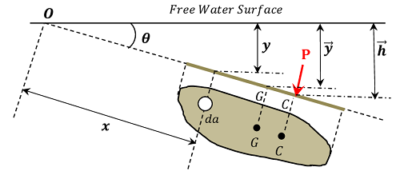
पत्रदल सतह कई सूक्ष्म क्षेत्रों ( elemental area ) से मिलकर बना हुआ है। इसी प्रकार के एक मौलिक क्षेत्र ( da ) पर विचार करें जो तरल कि सतह से ( y ) कि गहराई में स्थित है।
माना कि –
- ( w ) तरल का विशिष्ट भार ( specific weight ) है।
- ( \bar {y} ) तरल कि सतह से निमग्न पत्रदल का गुरुत्व केंद्र ( centre of gravity ) G की गहराई है।
तरल कि सतह से मौलिक क्षेत्र ( elemental area ) की गहराई ( y = x \sin \theta ) है।
\text {मौलिक क्षेत्र पर लगता हुआ कुल बल = मौलिक क्षेत्र से सीधे ऊपर के तरल के स्तंभ का वजन} = w \times ( da ) \times yअतः मौलिक क्षेत्र पर लगता हुआ दबाव = w \ y \ da होगा –
इस प्रकार, सतह पर लग रहे कुल दबाव को हम पुरे सतह पर integration की विधि से प्राप्त कर सकते हैं।
P = \sum {w \ y \ da} = w \sum {da \ y}
अतः \quad P = w A \bar y
Pressure on curved surface
वक्राकार सतह पर दबाव
एक वक्राकार ( curved ) सतह पर का दबाव ज्ञात करने के लिए सबसे पहले बल के क्षैतिज घटक ( horizontal component ) और ऊर्ध्वाधर घटक ( vertical component ) की गणना करते हैं। इसके पश्चात् कुल दबाव या परिणामी दबाव ( resultant pressure ) को ज्ञात करने के लिए उन्हें एक साथ संयुक्त कर लिया जाता है।
चित्र में दिखाए गए एक वक्राकार सतह AB पर विचार करें जो एक तरल में डूबा हुआ है। चित्र ( A ) में, तरल का दबाव वक्राकार सतह के अवतल पक्ष ( concave side ) पर है और चित्र ( B ) में, तरल का दबाव वक्राकार सतह के उत्तल पक्ष ( convex side ) पर है।
माना कि AB वक्राकार सतह का ऊर्ध्वाधर प्रक्षेपण ( vertical projection ) AC और क्षैतिज प्रक्षेपण ( horizontal projection ) BC है।
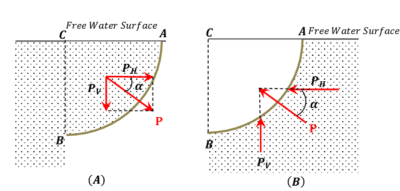
कुल दबाव का क्षैतिज घटक ( horizontal component ) ( P_H ) , वक्राकार सतह के क्षैतिज प्रक्षेपण BC पर लगता हुआ कुल क्षैतिज दबाव होगा और सतह के दबाव केंद्र ( centre of pressure ) के माध्यम से कार्य करेगा।
कुल दबाव का ऊर्ध्वाधर घटक ( vertical component ) (P_V) , वक्राकार सतह के ABC भाग में अवस्थित तरल के कुल वजन के बराबर होगा और उसके ( centre of gravity ) के माध्यम से कार्य करेगा।
अतः कुल दबाव या परिणामी दबाव को इस संबंध से प्राप्त किया जा सकता है –
P = \sqrt {{P_H}^2 + {P_V}^2}
कुल दबाव या परिणामी दबाव ( resultant pressure ) के झुकाव ( inclination ) को इस संबंध से प्राप्त किया जा सकता है –
\tan \alpha = \frac {P_V}{P_H}
जहां ( \alpha ) , कुल दबाव ( P ) और क्षैतिज घटक ( horizontal component ) ( P_H ) के बीच का कोण है।
कभी-कभी, वक्राकार सतह ( curved surface ) के निचले हिस्से पर द्रवस्थैतिक दबाव कार्य करता है जैसा कि चित्र ( B ) में दिखाया गया है, परन्तु इसके ऊपरी हिस्से पर इस तरह का कोई दबाव नहीं होता है। ऐसे मामलों में, ऊर्ध्वाधर दबाव ( vertical pressure ) ( P_V ) वक्राकार सतह से तरल की मुक्त सतह तक के तरल के काल्पनिक मात्रा के वजन के बराबर होगा। ऐसी अवस्था में ( P_V ) की दिशा ऊपर की ओर होती है।
