What is Lami’s Theorem?
लामिस का प्रमेय क्या है?
लामिस का प्रमेय ( Lami’s theorem ) एक त्रिकोणमितीय अभिव्यक्ति है जो साइन लॉ ( sin law ) का संसोधित रूप होता है। यह बलों ( forces ) से सम्बंधित संख्यात्मक प्रश्नों को हल करने में बहुत सहायक होता है।
Use of Lami’s theorem
लामिस का प्रमेय का उपयोग
लामिस का प्रमेय ( Lami’s theorem ) का उपयोग एकाधिक बलों की प्रणाली से सम्बंधित संख्यात्मक प्रश्नों को हल करने में बहुत लोकप्रिय है।
चित्र के अनुसार, एक वस्तु के O बिंदु पर विचार करें जिसपर 3 संगामी बल ( \vec {P} ), \ ( \vec {Q} ) और ( \vec {R} ) लग रहे हैं।
माना कि, उपरोक्त बलों के मान ( P ), \ ( Q ) और ( R ) हैं जो एक साथ वस्तु पर लग रहे हैं। चूंकि वस्तु स्थिर संतुलन ( static equilibrium ) में है।
इसलिए, ( P + Q + R ) = 0
बलों के triangle law of forces के अनुसार हम एक त्रिभुज ( \triangle ABC ) का निर्माण कर सकते हैं जिसकी भुजाएँ उपरोक्त बलों के आनुपातिक ( proportional ) होते हैं जैसा कि आरेख में दिखाया गया है।
त्रिभुज ( \triangle ABC ) कि भुजा AB, बल ( \vec {P} ) का प्रतिनिधित्व करता है। इसी प्रकार भुजा BC, बल ( \vec {Q} ) और भुजा CA, बल ( \vec {R} ) का प्रतिनिधित्व कर रहा है।
वेक्टर आरेख की ज्यामिति द्वारा हम त्रिभुज ( \triangle ABC ) के आंतरिक कोणों को ज्ञात कर सकते हैं।
अब, sin law कि मदद से हम लिख सकते हैं कि –
\left [ \frac {R}{\sin \left (180 - \alpha \right )} \right ] = \left [ \frac {P}{\sin \left (180 - \beta \right )} \right ] = \left [ \frac {Q}{\sin \left (180 - \gamma \right )} \right ]
इस संबंध को लामिस समीकरण ( Lami,s equation ) के रूप में जाना जाता है।

Sin Law
साइन लॉ
Sin law एक त्रिभुज की भुजाओं और उनके विपरीत आंतरिक कोणों के बीच त्रिकोणमितीय संबंध को स्थापित करता है। यह बताता है कि, एक त्रिभुज के किसी भुजा का माप और उस भुजा के विपरीत आतंरिक कोण की साइन के मान का अनुपात निश्चित होता है।
Proof of sin law
साइन लॉ का प्रमाण
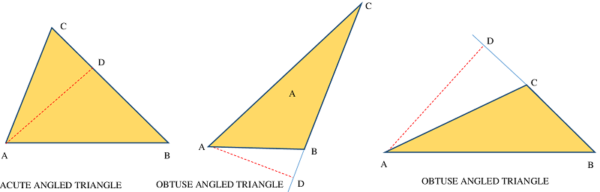
चित्र में दिखाए गए एक त्रिभुज ( \triangle ABC ) पर विचार करें जिसकी भुजाएँ ( AB = c ), \ ( BC = a ) और ( AC = b ) हैं।
शिखर बिंदु A से एक लम्ब AD खींचते हैं जो भुजा BC या उसके बढ़े हुए हिस्से को D बिंदु पर काटती है।
तब त्रिभुज की ऊंचाई AD = h है।
साइन लॉ की परिभाषा से हम पाते हैं कि –
\sin B = \left ( \frac {h}{c} \right )
और \quad \sin C = \left ( \frac {h}{b} \right )
या \quad h = c \sin B \quad और \quad h = b \sin C
इन सम्बन्धों की तुलना करने पर –
h = c \sin B = b \sin C
या, \quad \left ( \frac {c}{\sin C} \right ) = \left ( \frac {b}{\sin B} \right ) ……… (1)
पुनः लम्ब CD खींचते हैं जो भुजा AB या उसके बढ़े हुए हिस्से को D बिंदु पर काटती है।
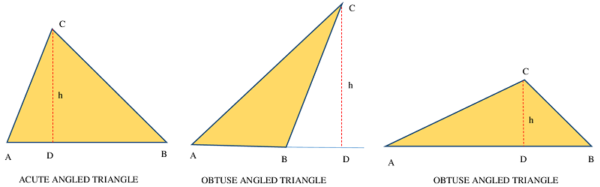
तब त्रिभुज की ऊंचाई CD = h है।
साइन लॉ की परिभाषा से हम पाते हैं कि –
\sin A = \left ( \frac {h}{c} \right )
और \quad \sin C = \left ( \frac {h}{a} \right )
या, \quad h = c \sin A \quad और \quad h = a \sin C
इन सम्बन्धों की तुलना करने पर –
\left ( \frac {c}{\sin C} \right ) = \left ( \frac {a}{\sin A} \right ) ……… (2)
समीकरण (1) और समीकरण (2) को मिलाने से हम पाते हैं –
\left ( \frac { \sin A }{ a } \right ) = \left ( \frac { \sin B }{ b } \right ) = \left ( \frac { \sin C }{ c } \right )
इस सम्बन्ध को साइन लॉ ( sin law ) कहा जाता है।
- यह सम्बन्ध किसी भी प्रकार के त्रिभुजों के लिए प्रयोज्य होता है।
- इसका उपयोग विज्ञान और इंजीनियरिंग में बलों से सम्बंधित संख्यात्मक प्रश्नों को हल करने में किया जाता है।
