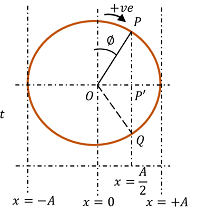What is called a Phasor diagram?
फेज़र आरेख क्या होता है?
फेज़र आरेख ( phasor diagram ) में समान आवृत्ति परन्तु अलग-अलग फेज़ कोणों और आयामों में सरल आवर्तीय गति ( Simple Harmonic Motion ) करने वाले कणों की स्थिति ( अर्थात phase ) का चित्रात्मक प्रदर्शन किया जाता है।
एक फेज़र आरेख ( phasor diagram ) का उपयोग करके सरल आवर्तीय गति करने वाले कणों की स्थितियों का विश्लेषण करना आसान हो जाता है। फेज़र आरेख ( phasor diagram ) बनाने के लिए हम इस प्रकार से आगे बढ़ते हैं –
पारम्परिक तरीके से यह मान लिया जाता है कि कण प्रारम्भ में माध्य स्थिति पर होता है। अर्थात ( t = 0 ) समय पर कण की स्थिति ( x = 0 ) बिंदु पर है। कण, दक्षिणावर्त दिशा में स्थिर वृत्तीय गति ( uniform circular motion ) से घूम रहा है।
तब, सरल आवर्तीय गति का सामान्य समीकरण इस प्रकार होगा –
x = A \sin ( \omega t + \phi _ { 0 } )
फेजर आरेखों का उपयोग करके संख्यात्मक समस्याओं का समाधान करना बहुत आसान हो जाता है जैसा कि निम्न उदाहरणों में दिया गया है –
EXAMPLE – 1
एक स्थिर वृत्तीय गति ( uniform circular motion ) से गतिमान कण के फेज़र आरेख ( phasor diagram ) पर विचार करें जो कि चित्र में दिखाया गया है। हमें इसकी गति का सामान्य समीकरण ( general equation of motion ) ज्ञात करना है।
दिखाए गए फेज़र आरेख की ज्यामिति से हम पाते हैं कि –

\phi _ { 0 } = 30 \degree = \left ( \frac { \pi }{ 6 } \right )
अतः कण की गति का सामान्य समीकरण होगा –
x = - A \sin ( \omega t + \phi _ { 0 } )
= - A \sin \left [ \omega t + \left ( \frac { \pi }{ 6 } \right ) \right ]
EXAMPLE – 2
मान लें कि एक कण की प्रारंभिक स्थिति \left ( x = + \frac{ A }{ 2 } \right ) पर है और यह धनात्मक ( x ) दिशा में गति कर रहा है। इसके गति के सामान्य समीकरण का निर्धारण करना है ।
- चित्र में कण की गति के लिए फेज़र आरेख तैयार किया गया है।
- मान ले कि कण वृत्तीय परिधि पर दक्षिणावर्त दिशा ( clockwise ) में घूम रहा है।
- कण की प्रारंभिक स्थिति \left ( x = + \frac{ A }{ 2 } \right ) स्थान पर है।
- इस परिस्थिति में कण की स्थिति P बिंदु पर या Q बिंदु पर में से कोई भी स्थान पर हो सकती है।
- परन्तु, कण घनात्मक ( x ) दिशा में आगे बढ़ रहा है। इसका तात्पर्य हुआ कि कण \left ( x = \frac {A}{2} \right ) से ( x = + A ) की दिशा में बढ़ रहा है।
- इसलिए, यह सुनिश्चित होता है कि कण प्रारम्भ में P बिंदु की स्थिति में है।
अतः फेजर आरेख ( phasor diagram ) को पूरा करते हैं। फेज़र आरेख से हमें प्राप्त होता है कि –
\left [ \frac { \left ( \frac { A }{ 2 } \right ) }{ A } \right ] = \cos \angle { POP' } = \left ( \frac { 1 }{ 2 } \right )
या, \quad \angle { POP' } = 60 \degree
अतः \quad \phi = \left ( 90 - 60 \right ) \degree = \left ( \frac { \pi }{ 6 } \right )
इस प्रकार, कण कि सरल आवर्तीय गति का समीकरण होगा –
x = A \sin \left [ \omega t + \left ( \frac { \pi }{ 6 } \right ) \right ]
Phase
फेज़
सरल आवर्तीय गति करने वाले कण के द्वारा संदर्भ बिंदु ( reference point ) से प्रतिस्थापित कोणीय विस्थापन ( angular displacement ) ( रेडियन में ) को फेज ( phase ) कहते हैं।
एक सरल आवर्त गति ( simple harmonic motion ) में जब कण अपनी चरम स्थिति ( अर्थात अधिकतम विस्थापन ) पर होता है तो वेग शून्य हो जाता है। साथ ही जब कण अपनी माध्य स्थिति ( शुन्य विस्थापन ) में होता है तो वेग अधिकतम होता है।
इसका मतलब यह हुआ कि, कण का अधिकतम वेग, कण के अधिकतम विस्थापन में पहुँचने से \left ( \frac {\pi}{2} \right ) रेडियंस पहले ही पूरा हो गया होता है। इसलिए, यदि हम विस्थापन और वेग को समय के अक्ष पर आरेख खींचते हैं, तो वेग का वक्र ( velocity curve ), विस्थापन के वक्र ( displacement curve ) से \left ( \frac {\pi}{2} \right ) रेडियंस आगे होगा। इस स्थिति को फेज़ ( phase ) शब्द के द्वारा व्यक्त किया जाता है।
इस प्रकार, वेग वक्र का फेज़ विस्थापन वक्र के फेज़ से \left ( \frac {\pi}{2} \right ) रेडियंस आगे रहता है।
Phase Angle
फेज कोण
एक कण के सरल आवर्तीय गति पर विचार करें। मान लीजिए कि ( t = 0 ) समय पर कण अपनी चरम की स्थिति ( x = +A ) से गति प्रारम्भ करता है। तब इसके गति समीकरण को इस प्रकार से लिखा जा सकता है –
x = A \cos \omega t …… विस्थापन ( Displacement ) समीकरण।
v = \left ( \frac { d x }{ d t } \right ) = - \omega A \sin \omega t ……. वेग ( Velocity ) समीकरण।
या, \quad v = \omega A \cos \left ( \omega t + \frac { \pi }{ 2 } \right )
a = \left ( \frac { d v }{ d t } \right ) = - \omega ^2 A \cos \omega t ……. त्वरण ( Acceleration ) समीकरण।
= \omega ^2 A \cos ( \omega t + \pi )
इन सभी समीकरणों में पद ( \omega t ) को फेज़ कोण ( phase angle ) के नाम से जाना जाता है।
सरल आवर्तीय गति की आवर्त काल ( time period ) की परिभाषा से हम पाते हैं कि –
T = \left ( \frac { 2 \pi }{ \omega } \right )
अतः किसी समय ( t = t ) पर फेज कोण ( phase angle ) का मान होगा –
\omega t = \left ( \frac { 2 \pi }{ T } \right ) t
\text {फेज कोण ( Phase angle )} = \text {समय ( Time )} \times \left ( \frac { 2 \pi }{\text {आवर्त काल ( Time period )}} \right )
Phase relationship in Simple Harmonic Motion
सरल आवर्तीय गति में फेज़ सम्बन्ध
सरल आवर्तीय गति के गुणों ( characteristics of simple harmonic motion ) को समझने के लिए हम ( x, \ v, \ \text {और} \ a ) के मान को चक्र के दौरान विभिन्न अवस्थाओं पर ज्ञात कर सकते हैं। इन मानों को नींचे दिया गया है।
| समय ( t ) | ( 0 ), \ ( T ) | \left ( \frac { T }{ 4 } \right ) | \left ( \frac { T }{ 2 } \right ) | \left ( \frac { 3T }{ 4 } \right ) |
| फेज़ कोण ( \omega t ) | ( 0 ), \ ( 2 \pi ) | \left ( \frac { \pi }{ 2 } \right ) | ( \pi ) | \left ( \frac { 3 \pi }{ 2 } \right ) |
| विस्थापन ( x ) | ( + A ) | ( 0 ) | ( - A ) | ( 0 ) |
| वेग ( v ) | ( 0 ) | \left ( - \omega A \right ) | ( 0 ) | ( + \omega A ) |
| त्वरण ( a ) | ( - \omega ^2 A ) | ( 0 ) | ( + \omega ^2 A ) | ( 0 ) |
इन मानों को एक ग्राफ पर आलेखित किया गया है जिसे फेज़ संबंध आरेख ( phase relationship diagram ) कहा जाता है।

- चित्र (A), समय के साथ विस्थापन का आरेख है।
- चित्र (B), समय के साथ वेग का आरेख है।
- चित्र (C), समय के साथ त्वरण का आरेख है।
Properties of Simple Harmonic Motion
सरल आवर्तीय गति के गुण
सरल आवर्तीय गति के गुणों को फेज़ संबंध आरेख ( phase relationship diagram ) से वर्णित किया जा सकता है।
ये गुण हैं –
- सरल आवर्तीय गति में विस्थापन ( displacement ), वेग ( velocity ) और त्वरण ( acceleration ) सभी समय के साथ आवर्तिय रूप से बदलते रहते हैं।
- अधिकतम वेग, अधिकतम विस्थापन या आयाम ( A ) का ( \omega ) के गुणा होता है।
- अधिकतम त्वरण, अधिकतम विस्थापन या आयाम ( A ) का ( \omega^2 ) के गुणा होता है।
- वेग वक्र का फेज़, विस्थापन वक्र के फेज से \left ( \frac {T}{4} \right ) या \left ( \frac {\pi}{2} \right ) रेडियंस आगे होता है। इसका तात्पर्य यह हुआ कि जिस पल में विस्थापन अधिकतम मान प्राप्त करता है उस समय वेग ने अपना अधिकतम मान \left ( \frac {\pi}{2} \right ) रेडियंस पहले ही पूरा कर लिया होता है। इसलिए, विस्थापन वक्र के मुकाबले वेग वक्र \left ( \frac {\pi}{2} \right ) रेडियंस से आगे रहता है।
- इस प्रकार वेग वक्र और विस्थापन वक्र के बीच का फेज़ अंतर ( phase difference ) \left ( \frac {\pi}{2} \right ) का होता है।
- जब विस्थापन शून्य होता है तब वेग अधिकतम होता है और इसके विपरीत जब वेग शून्य होता है तब विस्थापन अधिकतम होता है।
- त्वरण वक्र का फेज़, विस्थापन वक्र के फेज़ से \left ( \frac {T}{2} \right ) या \left ( \pi \right ) रेडियन आगे होता है। इसका तात्पर्य यह हुआ कि, जिस समय विस्थापन अधिकतम मान को प्राप्त करता है उस समय त्वरण ने अपना अधिकतम मान \left ( \pi \right ) रेडियंस पहले ही पूरा कर लिया होता है।
- इसलिए, विस्थापन वक्र के मुकाबले त्वरण वक्र \left ( \pi \right ) रेडियंस आगे रहता है। इस प्रकार त्वरण वक्र और विस्थापन वक्र के बीच का फेज़ अंतर \left ( \pi \right ) होता है।
- जब विस्थापन शून्य होता है तब त्वरण भी शून्य होता है।
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –