What is parallel axis theorem?
समानांतर अक्ष प्रमेय क्या होता है?
यदि किसी वस्तु के किसी अक्ष पर का जड़त्व आघूर्ण ज्ञात है, तो उसी तल पर अवस्थित एक अन्य समानांतर अक्ष पर का जड़त्व आघूर्ण एक साधारण संबंध द्वारा प्राप्त किया जा सकता है जिसे समानांतर अक्ष का प्रमेय ( parallel axis theorem ) कहा जाता है।
- समानांतर अक्ष प्रमेय ( parallel axis theorem ) किसी भी आकार के वस्तु के लिए मान्य होता है।
समानांतर अक्ष प्रमेय ( Parallel Axis Theorem ) यह प्रकट करता है की –
किसी ऐसी धुरी जो वस्तु के द्रब्यमान केंद्र ( centre of mass ) से गुजरने वाली धुरी के समानांतर है, उस धुरी पर एक वस्तु का जड़त्व आघूर्ण ( Moment of inertia ) द्रव्यमान केंद्र से गुजरने वाली धुरी पर आघूर्ण तथा क्षेत्र या द्रव्यमान के साथ दोनों अक्षों के बीच की दूरी के वर्ग के गुणनफल के योग के बराबर होता है।
क्षेत्र ( A ) वाले किसी वस्तु पर विचार करें जैसा कि चित्र में दिखाया गया है। दो अक्ष XX और YY अक्ष क्षेत्र के गुरुत्व केंद्र ( centre of gravity ) से गुजर रहे हैं। मान लें कि इन अक्षों पर क्षेत्र का जड़त्व आघूर्ण क्रमशः ( I_{xx} ) और ( I_{yy} ) हैं।
मान लें OX और OY अन्य दो अक्ष हैं जो XX अक्ष और YY अक्ष के समानांतर हैं जैसा कि चित्र में दिखाया गया है।
- तब, समानांतर अक्ष के प्रमेय ( parallel axis theorem ) के अनुसार, OX अक्ष पर क्षेत्र का जड़त्व आघूर्ण होगा –
I_{ox} = I_{xx} + A \left ( y^2 \right )
- इसी प्रकार, OY अक्ष पर क्षेत्र का जड़त्व आघूर्ण होगा –
I_{oy} = I_{yy} + A \left ( x^2 \right )
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –
MOI of a Rectangular section
आयताकार खंड का जड़त्व आघूर्ण
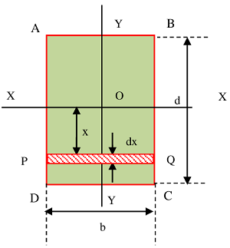
चित्र में दिखाए गए एक आयताकार खंड ABCD पर विचार करें।
खंड के लिए मान लें –
- चौड़ाई ( b ) अक्ष XX के सामानांतर है।
- गहराई ( d ) अक्ष YY के सामानांतर है।
- खंड X-Y तल पर अवस्थित है।
- अक्षों का मूल बिंदु गुरुत्व केंद्र ( centre of gravity ) O पर स्थित है।
खंड में ( dx ) मोटाई वाले एक सूक्ष्म पट्टी PQ पर विचार करें।
- पट्टी X अक्ष से x दूरी पर स्थित है।
सूक्ष्म पट्टी का क्षेत्रफल होगा –
dA = ( b \times dx ) = b \ dx
- पट्टी का XX अक्ष पर का जड़त्व आघूर्ण होगा –
101202 MOMENT OF INERTIA OF RECTANGULAR SECTION
dI = [ dA \times (\text {distance})^2 ]
= ( b \ dx ) ( x )^2 = b \ x^2 \ dx
अतः XX अक्ष पर आयताकार खंड का जड़त्व आघूर्ण होगा प्राप्त करने के लिए इस समीकरण को \left ( x = - \frac {d}{2} \right ) और \left ( x = + \frac {d}{2} \right ) लिमिट के बीच इंटीग्रेट करते हैं।
अतः, \quad I_{xx} = \left [ \int\limits_{- \frac {d}{2}}^{+ \frac {d}{2}} dI \right ]
= \left [ \int\limits_{- \frac {d}{2}}^{+ \frac {d}{2}} b \ x^2 \ dx \right ]
= b \left [ \int\limits_{- \frac {d}{2}}^{+ \frac {d}{2}} x^2 dx \right ]
= b \left [ \left ( \frac {x^3}{3} \right )_{- \frac {d}{2}}^{+ \frac {d}{2}} \right ]
= \left ( \frac {bd^3}{12} \right )
इसलिए, एक आयताकार खंड के (COG) से गुजरने वाले XX अक्ष पर का जड़त्व आघूर्ण \quad \left [ I_{xx} = \left ( \frac {bd^3}{12} \right ) \right ] होता है। यहाँ खंड का ( d ) किनारा, XX अक्ष के लंबवत होता है।
MOI of Rectangular Section about Base
आधार पर आयताकार खंड का जड़त्व आघूर्ण
- अक्ष XX पर आयत खंड का जड़त्व आघूर्ण होता है –
\quad I_{xx} = \left ( \frac {bd^3}{12} \right )
- Parallel Axis Theorem के अनुसार, आधार DC पर का जड़त्व आघूर्ण होगा –
\quad I_{base} = I_{xx} + A \ x^2
इसलिए, \quad I_{base} = \left [ \left ( \frac {bd^3}{12} \right ) + ( bd ) \ \left ( \frac {d}{2} \right )^2 \right ]
= \left [ \left ( \frac {bd^3}{12} \right ) + \left ( \frac {bd^3}{4} \right ) \right ]
= \left ( \frac {bd^3}{3} \right )
इसलिए, एक आयताकार खंड के आधार ( b ) पर का जड़त्व आघूर्ण \quad \left [ I_{base} = \left ( \frac {bd^3}{3} \right ) \right ] होता है।
गौर करें –
एक आयताकार खंड के जड़त्व आघूर्ण के लिए गणना में उस पक्ष के घन को लिया जाता है जो संदर्भ रेखा के लंबवत होता है जिस पर जड़त्व आघूर्ण की गणना की जा रही है।
MOI of a circular section
वृत्ताकार खंड का जड़त्व आघूर्ण
चित्र में दिखाए गए, ( r ) त्रिज्या और O केंद्र के एक वृत्ताकार खंड पर विचार करें जो XY तल पर स्थित है।
मान लें कि XX और YY अक्ष गुरुत्व केंद्र ( centre of gravity ) O से गुजर रहे हैं।
अब चित्र में दिखाए गए ( x ) त्रिज्या और ( dx ) मोटाई की एक सूक्ष्म वलय पर विचार करें।
- अत: सूक्ष्म वलय का क्षेत्रफल होगा –
dA = 2 \pi \ x \ dx
- इस वलय के तल पर लंबवत किसी अक्ष पर वलय का जड़त्व आघूर्ण ( Moment of inertia ) होगा –
dI = [ Area \times (\text {distance})^2 ]
या, \quad dI = ( 2 \pi \ x \ dx ) ( x )^2
= 2 \pi x^3 dx
इसलिए वृत्ताकार खंड के तल पर लंबवत किसी अक्ष पर पूरे खंड का जड़त्व आघूर्ण होगा –
I_{zz} = \int\limits_{0}^{r} dI
या, \quad I_{zz} = \left [ \int\limits_{0}^{r} 2 \pi x^3 dx \right ]
= \left [ 2 \pi \int\limits_{0}^{r} x^3 dx \right ]
= \left [ 2 \pi \left ( \frac {x^4}{4} \right )_{0}^{r} \right ]
= \left ( \frac {\pi r^4}{2} \right )
= \left ( \frac {\pi d^4}{32} \right )
क्योंकि \quad r = \left ( \frac {d}{2} \right )
इसलिए, एक वृत्ताकार खंड के तल पर लंबवत और खंड के (COG) से गुजरने वाले अक्ष पर का जड़त्व आघूर्ण \left [ I_{zz} = \left ( \frac {\pi d^4}{32} \right ) \right ] होता है। यहाँ ( d ) वृत्ताकार खंड का व्यास है ।
MOI of Circular Section about Diameter
व्यास पर वृत्ताकार खंड का जड़त्व आघूर्ण
- वृत्ताकार खंड के गुरुत्व केंद्र होकर खंड के तल पर लंबवत किसी अक्ष पर का जड़त्व आघूर्ण होता है –
\left [ I_{zz} = \frac {\pi d^4}{32} \right ] .
- लंबवत अक्ष प्रमेय ( perpendicular axis theorem ) से हम पाते हैं कि –
I_{zz} = ( I_{xx} + I_{yy} )
- परन्तु किसी वृत्ताकार खंड के लिए –
I_{xx} = I_{yy} ( सममिति के कारण )
अतः, \quad I_{xx} = I_{yy} = \left ( \frac {1}{2} \right ) \times \left ( I_{zz} \right )
इसलिए, \quad I_{xx} = I_{yy} = \frac {1}{2} \left ( \frac {\pi d^4}{32} \right )
या, \quad I_{xx} = I_{yy} = \left ( \frac {\pi d^4}{64} \right )
इसलिए, एक वृत्ताकार खंड के तल पर वृत्त के केंद्र से गुजरने वाले किसी अक्ष पर का जड़त्व आघूर्ण \left ( \frac {\pi d^4}{64} \right ) होता है। दूसरे शब्दों में , एक वृत्ताकार खंड के तल पर वृत्त के व्यास ( diameter ) पर का जड़त्व आघूर्ण \left ( \frac {\pi d^4}{64} \right ) होता है।
MOI of a Triangular section
आधार पर त्रिकोण खंड का जड़त्व आघूर्ण
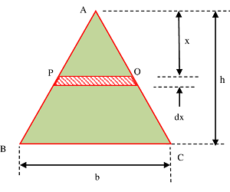
चित्र में दिखाए गए एक त्रिकोणीय खंड ABC पर विचार करें।
माना कि त्रिभुजाकार खंड के आधार BC का माप ( b ) है और खंड की ऊंचाई ( h ) है।
चित्र में दिखाए आधार के समानांतर और शिखर A से ( x ) की दूरी पर स्थित एक सूक्ष्म पट्टी PQ पर विचार करें। पट्टी की मोटाई ( dx ) है।
101204 MOMENT OF INERTIA OF TRIANGULAR SECTION चित्र कि ज्यामिति से प्राप्त होता हैं कि –
\triangle ABC and \triangle APQ समरूप त्रिभुज हैं।
- समरूप त्रिभुज के धर्म से प्राप्त होता है कि –
\left ( \frac {PQ}{BC} \right ) = \left ( \frac {x}{h} \right )
अतः, \quad PQ = BC \left ( \frac {x}{h} \right ) = \left ( \frac {bx}{h} \right )
- सूक्ष्म पट्टी का क्षेत्र होगा –
dA = ( PQ \times dx ) = \left ( \frac {bx}{h} \right ) dx
- त्रिकोण के आधार BC पर सूक्ष्म पट्टी का जड़त्व आघूर्ण होगा –
dI = [ Area \times (\text {Distance})^2 ]
या, \quad dI = \left ( \frac {bx}{h} \right ) dx \left ( h - x \right )^2
= \left ( \frac {bx}{h} \right ) \left ( h - x \right )^2 dx
- पूरे खंड का जड़त्व आघूर्ण होगा –
I_{base} = \int\limits_{0}^{h} dI
= \int\limits_{0}^{h} \left ( \frac {bx}{h} \right ) \left ( h - x \right )^2 dx
= \left ( \frac {b}{h} \right ) \int\limits_{0}^{h} x \left ( h^2 + x^2 - 2hx \right )dx
= \left ( \frac {b}{h} \right ) \int\limits_{0}^{h} \left ( xh^2 + x^3 - 2hx^2 \right ) dx
= \frac {b}{h} \left [ \frac {x^2h^2}{2} + \frac {x^4}{4} - \frac {2hx^3}{3} \right ]_{0}^{h}
= \left ( \frac {bh^3}{12} \right )
इसलिए, एक त्रिकोणीय खंड के आधार से गुजरने वाले किसी अक्ष पर का जड़त्व आघूर्ण \left [ I_{base} = \left ( \frac {bh^3}{12} \right ) \right ] होता है। जहाँ ( b ) त्रिकोण के आधार का माप और ( h ) त्रिकोण कि ऊंचाई है।
MOI of Triangular Section about COG
केंद्रीय अक्ष पर त्रिकोण खंड का जड़त्व आघूर्ण
- एक त्रिभुजाकार खंड का उसके आधार पर का जड़त्व आघूर्ण होता है –
I_{base} = \left ( \frac {bh^3}{12} \right )
- किसी त्रिभुज का गुरुत्व केंद्र ( centre of gravity ) आधार से \left ( \frac {h}{3} \right ) ऊंचाई पर स्थित होता है।
अतः त्रिभुज के आधार रेखा BC और XX अक्ष के बीच की दूरी होगी –
d = \left ( \frac {h}{3} \right )
- इसलिए, समानांतर अक्ष प्रमेय के अनुसार –
I_{base} = I_{xx} + A d^2
या, \quad I_{xx} = I_{base} - A d^2
NOTE :- यहां ऋण चिह्न इसलिए लिया जाता है क्योंकि XX अक्ष में प्रभावी क्षेत्र वितरण, BC से गुजरने वाले अक्ष के प्रभावी क्षेत्र वितरण की तुलना में घट रहा है।
- इसलिए, \quad I_{xx} = \left ( \frac {bh^3}{12} \right ) - \left ( \frac {b h}{2} \right ) \left ( \frac {h}{3} \right )^2
या, \quad I_{xx} = \left ( \frac {bh^3}{36} \right )
इसलिए, खंड के तल पर स्थित त्रिभुज के आधार के समानांतर और गुरुत्व केंद्र से गुजरने वाले त्रिकोणीय खंड का जड़त्व आघूर्ण \left ( \frac {bh^3}{36} \right ) होता है।
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –