What is Moment of Inertia?
जड़त्व आघूर्ण क्या होता है?
पिछले लेखों में हमने बल आघूर्ण ( moment of force ) के बारे में जाना है। इस लेख में, हम आघूर्ण की जड़ता के बारे में चर्चा करेंगे जिसे जड़त्व आघूर्ण ( Moment of Inertia ) कहा जाता है।
वह भौतिक गुण जिसके कारण वस्तु किसी वृत्ताकार पथ में गति, अर्थात वक्रता गति या घूर्णन गति ( curvilinear motion or rotary motion ) की स्थिति में परिवर्तन का विरोध करता है उसे आघूर्ण की जड़ता ( Inertia of moment ) या जड़त्व आघूर्ण ( Moment of inertia ) कहा जाता है।
किसी वस्तु का जड़त्व आघूर्ण तभी कार्य करते हुए गति में परिवर्तन का विरोध करता है जब –
- यदि वस्तु वृत्ताकार पथ ( circular motion ) या घुमावदार ( curved path ) पथ पर गति में है।
- यदि वस्तु किसी अक्ष या बिंदु को केंद्र मानकर घूम रहा है।
जड़त्व आघूर्ण को दूसरा आघूर्ण ( Second Moment ) या आघूर्ण का आघूर्ण ( Moment of Moment ) भी कहा जाता है।
- संक्षेप में जड़त्व आघूर्ण को ( MI ) लिखा जाता है।
Types of Moment of Inertia
जड़त्व आघूर्ण के प्रकार
मूलतः जड़त्व आघूर्ण तीन प्रकार का होता है –
1. बल का जड़त्व आघूर्ण ( Force moment of inertia )
- यह बल आघूर्ण का आघूर्ण होता है।
- इसका मान \left ( F x^2 \right ) से दर्शाया जाता है।
- यहाँ ( F ) बल की मात्रा है और ( x ) घूमने के अक्ष से बल के क्रिया रेखा की लंबवत दूरी है।
2. क्षेत्र का जड़त्व आघूर्ण (Area moment of inertia )
- यह किसी क्षेत्र का आघूर्ण होता है।
- इसका मान \left ( A x^2 \right ) से दर्शाया जाता है।
- यहाँ ( A ) किसी दो आयामी वस्तु जैसे पटल ( lamina ) का क्षेत्रफल है और ( x ) घूमने के अक्ष से पटल के केन्द्रक ( centroid ) की दूरी है।
3. द्रब्यमान का जड़त्व आघूर्ण ( Mass moment of inertia )
- यह किसी द्रब्यमान का आघूर्ण होता है।
- इसका मान \left ( M x^2 \right ) से दर्शाया जाता है।
- यहाँ ( M ) वस्तु का द्रब्यमान है और ( x ) घूमने के अक्ष से वस्तु के गुरुत्व केंद्र ( centre of gravity ) की दूरी है।
इस विषय पर आधारित संख्यात्मक प्रश्न देखें –
Radius of Gyration
परिक्रमण त्रिज्या
- किसी अक्ष के चारों ओर घूमने वाले ( M ) द्रव्यमान के एक वस्तु पर विचार करें।
- वस्तु को ( m_1, \ m_2 \ ..... \ m_n ) इत्यादि कई छोटे द्रव्यमान कणों से मिलकर बना माना जा सकता है।
- अतः वस्तु का द्रब्यमान \quad M = ( m_1 + m_2 + ........ + m_n ) = \sum {m} है।
- माना कि घूर्णन अक्ष से छोटे द्रब्यमानों की दूरी क्रमशः ( r_1, \ r_2 \ ...... \ r_n ) आदि हैं।
अतः, छोटे छोटे द्रब्यमानों के पृथक जड़त्व आघूर्ण ( m_1 r_1^2, \ m_2 r_2^2 \ ......... \ m_n r_n^2 ) आदि होंगे।
- अत: पूरे वस्तु का जड़त्व आघूर्ण होगा –
MI = ( m_1 r_1^2 + \ m_2 r_2^2 + ........ + \ m_n r_n^2 ) = \sum {mr}^2
वस्तु के जड़त्व आघूर्ण के मान को द्रब्यमान M के रूप में इस प्रकार दर्शाया जा सकता है।
- जड़त्व आघूर्ण \quad MI = \sum {mr}^2 = M \ k^2
तब ( k ) को वस्तु का परिक्रमण त्रिज्या ( radius of gyration or swing radius ) कहा जाता है।
इसलिए, किसी वस्तु के परिक्रमण त्रिज्या को एक काल्पनिक वृत्ताकार वलय की त्रिज्या के रूप में परिभाषित किया जा सकता है जिसका द्रव्यमान उस वस्तु के द्रव्यमान के बराबर होता है।
- अतः, परिक्रमण त्रिज्या \quad k = \sqrt { \frac { \sum {mr}^2 }{ M } } = \sqrt {\frac { M I }{ M }}
इसी प्रकार से क्षेत्र जड़त्व आघूर्ण के लिए –
- परिक्रमण त्रिज्या \quad k = \sqrt { \frac { \sum {ar}^2 }{ A } } = \sqrt {\frac { M I }{ A }}
जहाँ कुल क्षेत्र \quad A = ( a_1 + a_2 + ....... + a_n ) = \sum a
Routh’s Rule
रॉथ का नियम
तीन आयामी सममित ठोस वस्तुओं की जड़त्व आघूर्ण को प्राप्त करने के लिए रॉथ का नियम एक सामान्य नियम है।
- रॉथ का नियम दो आयामी ( two dimensional ) वस्तुओं के लिए मान्य नहीं होता है।
यह नियम सिर्फ –
- तीन आयामी ( three dimensional solids ) ठोस वस्तुओं के लिए लागू होता है।
- वे वस्तुएं जो तीनों अक्षों, अर्थात X , Y और Z में सममित होते हैं, उनपर लागू होता है। उदाहरण – वृत्ताकार या अण्डाकार बेलन, घनाभ, वृत्ताकार डिस्क आदि जो किसी सममिति अक्ष के परितः घूर्णन कर रहे हैं।
रॉथ का नियम यह बताता है कि –
(1) किसी क्षेत्र का जड़त्व आघूर्ण ( Area Moment of Inertia ) ( A ) होता है –
MI = A \left [ \frac {\text {Sum of squares of perpendicular axes}}{3, \ 4 \ or \ 5} \right ]
(2) किसी द्रब्यमान का जड़त्व आघूर्ण ( Mass moment of inertia ) ( M ) होता है –
MI = M \left [ \frac {\text {Sum of squares of perpendicular axes}}{3, \ 4 \ or \ 5} \right ]
इन समीकरणों में ( 3, \ 4, \ 5 ) संख्याओं को वस्तु के आकार के आधार पर लिया जाता है। ये इस प्रकार हैं –
- किसी वर्गाकार वस्तु या पटल ( lamina ) के लिए ( 3 )
- किसी वृत्ताकार ( circular ) या अण्डाकार ( elliptical ) वस्तु या पटल ( lamina ) के लिए ( 4 )
- किसी गोलाकार ( spherical ) या अण्डाकार गोले ( ellipsoidal ) के लिए ( 5 )
ILLUSTRATION
चित्र में दिखाए गए एक अण्डाकार पटल पर विचार करें।

इस वस्तु के लिए X और Y दिशाओँ में अक्ष क्रमशः ( a ) और ( b ) हैं।
इसलिए, अक्षों का योग \left ( a^2 + b^2 \right ) है और हर ( denominator ) में हम अण्डाकार पटल के लिए ( 4 ) का उपयोग करते हैं।
अत: रॉथ के नियम से अण्डाकार पटल का जड़त्व आघूर्ण होगा –
MI_Z = A \left ( \frac { a^2 + b^2 }{ 4 } \right )
MOI of common Objects
साधारण वस्तुओं का जड़त्व आघूर्ण
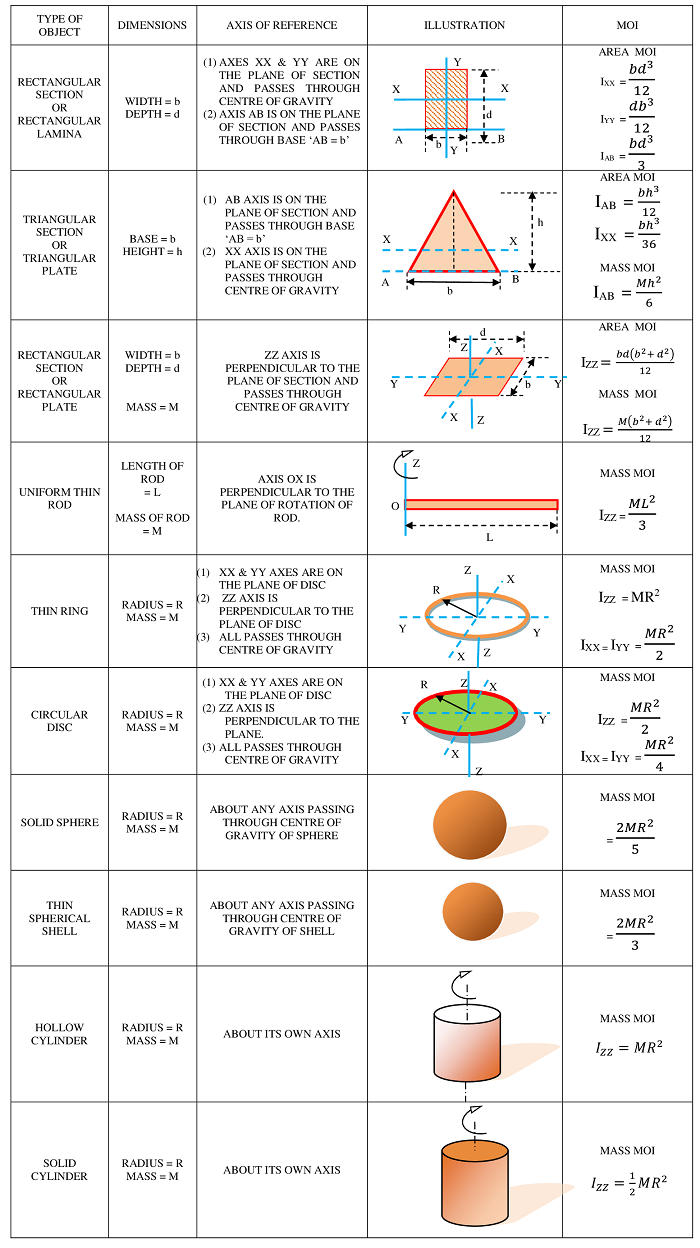
विभिन्न अक्षों में सरल ज्यामितीय आकृतियों वाली वस्तुओं के लिए जड़त्व आघूर्ण की एक तुलनात्मक सूची नीचे दी गई है, ताकि समान वस्तुओं के बीच जड़त्व आघूर्ण मूल्यों की तुलना को अलग किया जा सके और उपयोग के समय आसानी से याद किया जा सके।
Steps to find Moment of Inertia
जड़त्व आघूर्ण ज्ञात करने की विधी
किसी अनियमित आकार की वस्तु का जड़त्व आघूर्ण ज्ञात करने के लिए integration विधि का उपयोग करते हैं। इसमें निम्नलिखित चरण शामिल हैं –
STEP 1 – DRAW A SKETCH AND CO-ORDINATE AXES
वस्तु का एक साफ-सुथरा स्केच बनाएं। इसके लिए बिना किसी स्केल का एक अपरिष्कृत चित्र ( rough sketch ) पर्याप्त होता है। संदर्भ के लिए X अक्ष और Y अक्ष और मूल बिंदु O का चित्रण करें।
हमें XX' और YY' अक्षों से वस्तु की जड़त्व आघूर्ण का मान को ज्ञात करना है।
STEP 2 – CUT AN ELEMENTARY STRIP
सर्वप्रथम YY' अक्ष के समानांतर दो कटिंग प्लेन की कल्पना करें। मान लें कि ये कटिंग प्लेन अक्ष से \left ( x \right ) और \left ( x + dx \right ) की दूरी से गुजर रहे हैं। इस प्रकार, एक सूक्ष्म पट्टी ABCD को काटा जाता है जैसा कि चित्र में छायांकित क्षेत्र से दिखाया गया है।

सूक्ष्म पट्टी की चौड़ाई ( dx ) होगी। मान लें की लम्बाई ( L ) है।
चूँकि, ( dx ) बहुत छोटा है इसलिए क्षेत्र ABCD एक आयत क्षेत्र माना जा सकता है।
- सूक्ष्म पट्टी ABCD का क्षेत्रफल dA = ( L \times dx ) .
इस समीकरण में लम्बाई ( L ) परिवर्तनीय है जो YY' अक्ष से कटिंग प्लेन की दूरी ( x ) पर निर्भर होता है।
अब, ज्यामिती का प्रयोग करके लम्बाई ( L ) को दूरी ( x ) के रूप में व्यक्त करते हैं।
STEP 3 – FIND COG & MI FOR ELEMENTARY STRIP
चूंकि सूक्ष्म पट्टी ABCD ] एक आयत है, इसलिए पट्टी की ( COG ) की दूरी YY' अक्ष से \left ( x + \frac {dx}{2} \right ) पर होगी।
लेकिन ( dx ) बहुत छोटा है। इसलिए \left ( \frac {dx}{2} \right ) को नगन्य माना जा सकता है।
अतः \quad \left ( x + \frac {dx}{2} \right ) = x
अब, YY' अक्ष पर सूक्ष्म पट्टी का जड़त्व आघूर्ण होगा -
dM = \left ( dA \ x \right ) x = x^2 \ dA = x^2 \ L \ dx
STEP 4 - DIVIDE WHOLE OBJECT INTO NUMEROUS STRIPS
इसी प्रकार के समानांतर कटिंग प्लेनों का उपयोग करते हुए पूरी वस्तु को कई सूक्ष्म पट्टियों में कटा हुआ माना जाता है। इन कटिंग प्लेनों के लिए दूरी ( x ) अलग-अलग पट्टियों के लिए अलग-अलग होगी। यह \left ( x = a \right ) से \left ( x = b \right ) के बीच होगा।
इसलिए, सूक्ष्म पट्टियों के लिए जड़त्व आघूर्ण का मान होगा -
dM_1 = \left ( x_1 \right )^2 dA_1, \quad dM_2 = \left ( x_2 \right )^2 dA_2 \quad .... आदि।
जहाँ, ( dA_1 ), \ ( dA_2 ) \ ...... आदि विभिन्न सूक्ष्म पट्टियों के क्षेत्रफल हैं।
STEP 5 - APPLY INTEGRATION METHOD
वस्तु का कुल जड़त्व आघूर्ण प्रत्येक पट्टी के लिए सूक्ष्म जड़त्व आघुर्णो का योग होगा।
इसलिए, \quad MI = ( dM_1 + dM_2 + \ .... + dM_n )
या, \quad MI = \sum {dM}
या, \quad MI = \sum_{a}^{b} x^2 \ dA
अब, YY' अक्ष से वस्तु का जड़त्व आघूर्ण MI को प्राप्त करने के लिए इंटिग्रेशन विधि को लागू करते हैं -
MI_{yy} = \int\limits_{b}^{a} x^2 \ dA
जहाँ ( a ) और ( b ) वस्तु आयाम का X अक्ष पर न्यूनतम और अधिकतम मान हैं।
उपर्युक्त समीकरण को इंटीग्रेट करके YY' अक्ष पर वस्तु का ( MI ) को हम प्राप्त कर सकते हैं।
इसी प्रकार, चरण 1 से 5 को दोहरा कर XX अक्ष पर वस्तु के ( MI ) को प्राप्त कर सकते हैं।
इस विषय पर आधारित संख्यात्मक प्रश्न देखें -
