What is Screw Jack?
स्क्रू जैक क्या होता है?
स्क्रू जैक ( screw Jack ) एक लिफ्टिंग मशीन है जो एक स्क्रू ( screw ) के सिद्धांत पर काम करती है। इसका उपयोग बड़े भार को उठाने के लिए किया जाता है।
यह लिफ्टिंग मशीन ( lifting machine ) का सबसे सरल रूप है।
Working principle of a screw jack
स्क्रू जैक के कार्य का सिद्धांत
स्क्रू जैक, एक स्क्रू के सिद्धांत पर कार्य करता है जो कि एक झुके हुए तल ( inclined plane ) के सिद्धांत का उपयोग करता है।
चित्र में दिखाए गए स्क्रू जैक पर विचार करें।
यदि स्क्रू की एक चूड़ी को खोलकर एक समतल सतह पर रखा जाए तो यह एक झुका हुआ तल बनता है जैसा की चित्र में दिखाया गया है।
माना कि –
- स्क्रू के चूड़ी की पिच ( pitch ) ( p ) है।
- स्क्रू का औसत व्यास ( mean diameter ) ( D ) है।
- स्क्रू का हेलिक्स कोण ( helix angle ) या प्रक्षेपित झुके हुए तल का झुकाव कोण ( inclination ) ( \alpha ) है।
- स्क्रू के पदार्थ का घर्षण कोण ( angle of friction ) ( \phi ) है।
लोड को स्क्रू हेड ( screw head ) पर रखा जाता है और उसकी परिधि पर एक लंबी रॉड या लीवर के सहारे प्रयास बल ( Effort ) लगाया जाता है।
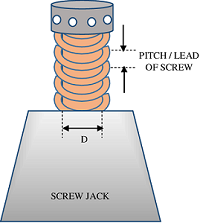
स्क्रू के एक पुरे घुमाव में हम पाते हैं –
- प्रयास के द्वारा तय दूरी = \pi D
- लोड के द्वारा तय दूरी = p
अतः स्क्रू जैक का वेलॉसिटी रेसिओ ( Velocity ratio ) \left ( \frac {\pi D}{p} \right ) होगा।
चित्र में, स्क्रू के प्रक्षेपित ( projected ) झुके हुए तल पर विचार करने पर –
\tan \alpha = \left ( \frac { p }{ \pi D } \right )
Efficiency of screw jack
स्क्रू जैक की दक्षता
किसी मशीन में, आउटपुट कार्य और इनपुट कार्य के अनुपात को दक्षता ( Efficiency ) कहा जाता है। इसलिए स्क्रू जैक की दक्षता –
\eta = \frac{\text {आउटपुट कार्य}}{\text {इनपुट कार्य}}
दक्षता को दूसरे तरीके से भी परिभाषित किया जाता है –
\eta = \frac{\text {आदर्श प्रयास बल}}{\text {वास्तविक प्रयास बल}}
अब स्क्रू के घर्षण बल ( force of friction ) पर विचार करने पर हमें घर्षण के निम्नलिखित प्रभाव मिलते हैं –
- जब लोड को उठाया जाता है तो घर्षण बल नीचे की ओर कार्य करता है। यहाँ घर्षण बल, लोड की गति के विपरीत दिशा में कार्य कर रहा है। इसलिए, आवश्यक प्रयास बल बढ़ जाता है।
- जब लोड को निचे किया जाता है तो घर्षण बल ऊपर की ओर कार्य करता है। इस बार घर्षण बल, लोड के गति की दिशा में कार्य करता है। इसलिए, आवश्यक प्रयास बल कम हो जाता है।
इस प्रकार लोड को उठाने के लिए आवश्यक प्रयास बल होगा –
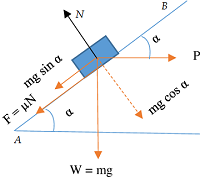
P _ {Rising} = W \tan \left ( \phi + \alpha \right ) .
और लोड को निचे करने के लिए आवश्यक प्रयास बल होगा –
P _ {Lowering} = W \tan \left ( \phi - \alpha \right )
जब घर्षण नगण्य होने पर, घर्षण कोण ( angle of friction ) ( \phi ) का मान शुन्य हो जाता है।
अतः, लोड को उठाने के समय जैक की आदर्श दक्षता ( ideal efficiency ) होगी –
P_{Ideal} = W \tan \alpha
इसलिए लोड को उठाने के समय, जैक की वास्तविक दक्षता ( efficiency ) होगी –
\eta = \left [ \frac {W \tan \alpha}{W \tan (\alpha + \phi)} \right ]
अतः \quad \eta_{Rising} = \left [ \frac {\tan \alpha}{\tan (\alpha + \phi)} \right ]
Maximum efficiency of screw jack
स्क्रू जैक की अधिकतम दक्षता
जैक की दक्षता समीकरण इस प्रकार होती है –
\eta = \left [ \frac {\tan \alpha}{\tan (\alpha + \phi)} \right ]
= \left [ \left ( \frac {\sin \alpha}{\cos \alpha } \right ) \div \left ( \frac {\sin ( \alpha + \phi)}{\cos ( \alpha + \phi )} \right ) \right ]
= \left [ \frac{ \sin \alpha \times \cos \left ( \alpha + \phi \right ) }{ \cos \alpha \times \sin \left ( \alpha + \phi \right ) } \right ]
भाज्य ( numerator ) और भाजक ( denominator ) दोनों को 2 से गुणा करने पर –
\eta = \left [ \frac { 2 \sin \alpha \times \cos \left ( \alpha + \phi \right ) }{ 2 \cos \alpha \times \sin \left ( \alpha + \phi \right ) } \right ]
त्रिकोणमिती से –
- \quad \left [ \sin ( A + B ) + \sin ( A - B ) = 2 \sin A \cos B \right ]
- \quad \left [ \sin ( A + B ) - \sin ( A - B ) = 2 \cos A \sin B \right ]
इसलिए, स्क्रू जैक की दक्षता इस प्रकार होगी –
\eta = \left [ \frac { \sin \left ( 2 \alpha + \phi \right ) - \sin \phi }{ \sin \left ( 2 \alpha + \phi \right ) + \sin \phi } \right ]
या, \quad \left [ \left ( 1 - \eta \right ) \right ] = \left [ 1 - \frac { \sin \left ( 2 \alpha + \phi \right ) - \sin \phi }{ \sin \left ( 2 \alpha + \phi \right ) + \sin \phi } \right ]
= \left [ \frac { 2 \sin \phi }{ \sin \left ( 2 \alpha + \phi \right ) + \sin \phi } \right ]
समीकरण से यह स्पष्ट होता हैं कि, दक्षता अधिकतम होगी, जब \left ( 1 - \eta \right ) का मान न्यूनतम होगा।
किसी विशेष स्क्रू के लिए ( \phi ) एक नियतांक होता है क्योंकि वह पदार्थ पर निर्भर करता है।
अतः \left ( 1 - \eta \right ) का मान न्यूनतम तब होगा, जब [ \sin \left ( 2 \alpha + \phi \right ) ] का मान अधिकतम होगा।
इसलिए दक्षता समीकरण में, [ \sin \left ( 2 \alpha + \phi \right ) ] का संभावित अधिकतम मान ( 1 ) रखने पर –
अधिकतम दक्षता –
\eta _ {Max} = \left [ \frac { \sin \left ( 2 \alpha + \phi \right ) - \sin \phi }{ \sin \left ( 2 \alpha + \phi \right ) + \sin \phi } \right ]
= \left [ \frac { 1 - \sin \phi }{ 1 + \sin \phi } \right ]
Overhauling of Screw Jack
स्क्रू जैक का ओवरहालिंग
लोड को निचे करने के समय, आवश्यक प्रयास बल ( P ) का मान इस प्रकार होता है –
P = W \tan \left ( \phi - \alpha \right )
उपरोक्त व्यंजक में, यदि ( \phi < \alpha ) हो, तब समीकरण के अनुसार, लोड को निचे करने के लिए आवश्यक प्रयास बल ऋणात्मक होगा। अन्य शब्दों में यह कहा जा सकता है कि, बिना किसी प्रयास के लोड स्वतः नीचे की ओर उतरता है।
ऐसी स्थिति को, स्क्रू का ओवरहालिंग ( overhauling of a screw ) कहा जाता है और ऐसे मशीन को रिवर्सिबल मशीन ( reversible machine ) कहा जाता है।
एक लिफ्टिंग मशीन को रिवर्सिबल मशीन तब कहा जाता है जब वह लोड उठाने के लिए लगाए गए प्रयास को हटा देने पर विपरीत दिशा में कार्य करने लगता है।
किसी लिफ्टिंग मशीन के लिए रिवर्सिबिलिटी, वांछनीय गुण नहीं होता है। जब प्रयास को हटा लिया जाता है तब लोड अपने आप निचे गिरने लगता है जिसके कारन दुर्घटना घट सकती है और उपकरण क्षतिग्रस्त हो सकता है।
यदि ( \phi > \alpha ) होता है तब समीकरण के अनुसार लोड को निचे करने के लिए, आवश्यक प्रयास बल घनात्मक होगा। अर्थात, लोड को निचे करने के लिए एक प्रयास बल की आवश्यकता होगी। ऐसे स्क्रू को सेल्फ लॉकिंग ( self locking ) स्क्रू कहा जाता है।
इसलिए, कोई भी लिफ्टिंग मशीन ( lifting machine ), सेल्फ लॉकिंग होनी चाहिए।
अतः सेल्फ लॉकिंग के लिए, घर्षण कोण ( \phi ) को हेलिक्स कोण ( \alpha ) के मान से बड़ा होना होगा।
मान लें कि, किसी लोड को उठाने के लिए वास्तविक प्रयास बल ( P_{Actual} ) है और घर्षण को उपेक्षित करने पर आदर्श प्रयास बल ( P_{Ideal} ) है।
तब स्क्रू जैक का वेलॉसिटी रेसिओ होगा –
VR = \left ( \frac { W }{ P_ { Ideal }} \right )
या \quad ( P _ { Ideal } ) = \left ( \frac { W }{ VR } \right )
और घर्षण में नष्ट हुआ प्रयास बल होगा –
( P _ { Friction } ) = ( P _ { Actual } - P _ { Ideal } ) = \left [ P _ { Actual } - \left ( \frac { W }{ VR } \right ) \right ]
जब प्रयास बल को हटा लिया जाता है तब लोड को स्वतः नीचे गिरने से रोकने वाला बल, घर्षण बल होता है। यह घर्षण बल \left [ P _ { Actual } - \left ( \frac { W }{ VR } \right ) \right ] के बराबर होता है।
जब घर्षण बल, प्रयास बल ( P_{Ideal} ) के मान से अधिक होता है तब प्रयास को हटा लेने पर भी लोड ( W ) स्वतः निचे नहीं गिरता है।
इसलिए, प्रयास बल कि अनुपस्थिति में, लोड को संतुलन में रखने के लिए आवश्यक घर्षण बल कि मात्रा \left [ P _ { Actual } - \left ( \frac { W }{ VR } \right ) \right ] होती है।
अत: किसी मशीन के सेल्फ लॉकिंग के लिए आवश्यक शर्त है –
( P _ { Friction } ) > ( P _ { Ideal } )
या \quad ( P _ {Actual} - P _ {Ideal} ) > ( P _ {Ideal} )
अतः \quad ( P _ {Actual} ) > 2 ( P _ {Ideal} )
इसलिए, एक सेल्फ लॉकिंग मशीन में किसी लोड को उठाने के लिए वास्तविक प्रयास बल, आदर्श प्रयास बल के दोगुने से अधिक होता है।
Condition of self locking
सेल्फ लॉकिंग की शर्त
सेल्फ लॉकिंग की आवश्यक शर्त इस प्रकार है –
( P _ {Actual} ) > 2 ( P _ {Ideal} )
या, \quad \left ( \frac {P _ {Actual}}{P _ {Ideal}} \right ) > 2
अथवा \quad \left ( \frac {P _ {Ideal}}{P _ {Actual}} \right ) < \left ( \frac {1}{2} \right )
परन्तु पद \left ( \frac { P_{Ideal}}{P_{Actual}} \right ) को मशीन कि दक्षता ( efficiency ) कहते हैं।
अतः, सेल्फ लॉकिंग के लिए मशीन कि दक्षता इस प्रकार होनी चाहिए –
\eta < \left ( \frac {1}{2} \right )
