How friction works on inclined plane?
झुके हुए तल पर घर्षण बल कैसे कार्य करता है?
झुके हुए तल पर घर्षण ( friction on inclined plane ), तल के झुकाव कोण ( angle of inclination ) पर निर्भर करता है। जैसे-जैसे झुकाव कोण का मान बढ़ता जाता है, घर्षण बल का प्रभाव घटता जाता है।
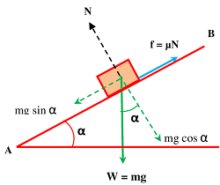
इसे समझने के लिए, चित्र में दिखाए गए एक ठोस ब्लॉक पर विचार करें जो एक समायोज्य झुकाव वाले तल ( adjustable inclined plane ) AB पर रखा गया है। माना की वस्तु का द्रब्यमान ( mass ) ( m ) और तल का झुकाव क्षैतिज से ( \alpha ) कोण में है।
इस स्थिति में वस्तु के भार का आयताकार घटकों ( rectangular components ) का मान निम्न होगा –
- तल के सामानांतर वस्तु के भार का घटक ( mg \sin \alpha ) है।
- तल के लंबवत वस्तु के भार का घटक ( mg \cos \alpha ) है।
तल के समानांतर लगने वाला घटक ( mg \sin \alpha ) वस्तु को नींचे फिसलने में मदद करता है, परन्तु उत्पन्न घर्षण बल ( f ) के कारण वस्तु स्थिर रहती है।
अब, तल के झुकाव कोण ( \alpha ) को धीरे-धीरे बढ़ाया जाता है। एक स्थिति ऐसी आती है जब ब्लॉक तल पर नींचे खिसकने को तत्पर होता है।
इस स्थिति में, निम्न बलों के प्रभाव से वस्तु संतुलन ( equilibrium ) में होता है –
- तल के सामानांतर, वस्तु के भार का घटक ( mg \sin \alpha ) । यह तल के सामानांतर नींचे की ओर कार्य करता है।
- वस्तु और तल के संस्पर्श सतह पर लगता हुआ घर्षण बल ( f ) । चूँकि वस्तु नींचे कि ओर खिसकना चाहती है, इसलिए घर्षण बल, ऊपर की ओर कार्य करता है।
- तल के लंबवत, अभिलम्ब प्रतिक्रिया ( normal reaction ) का मान ( N ) ।

021501 MOTION OF BODY ON INCLINED PLANE
चूँकि वस्तु स्थिरावस्था में है। अतः संतुलन ( equilibrium ) के लिए –
N = mg \cos \alpha
अतः, अभिलम्ब प्रतिक्रिया का मान, झुके हुए तल के झुकाव कोण पर निर्भर करता है।
फिर, \quad f = mg \sin \alpha
चित्र की ज्यामिति से हम पाते हैं कि –
- लम्ब प्रतिक्रिया ( N ) और वस्तु के भार ( W = mg ) के बीच का कोण ( 180 \degree - \alpha ) है।
- घर्षण बल ( f ) और वस्तु के भार ( W = mg ) के बीच का कोण ( 90 \degree + \alpha ) है।
अब, लामिस का प्रमेय ( lami’s theorem ) का उपयोग करके हम पाते हैं कि –
\left [ \frac {N}{\sin \left (90 \degree + \alpha \right )} \right ] = \left [ \frac {f}{\sin \left (180 \degree - \alpha \right )} \right ]
परन्तु, \quad f = \mu N
इस प्रकार से, जैसे-जैसे झुकाव कोण का मान बढ़ता है, अभिलम्ब प्रतिक्रिया घटने से घर्षण बल का प्रभाव घटता जाता है।
Relation between Angle of inclination and Angle of friction
झुकाव का कोण और घर्षण कोण में सम्बन्ध
लामिस का प्रमेय ( lami’s theorem ) का उपयोग करके हम पाते हैं कि –
\left [ \frac {N}{\sin \left (90 \degree + \alpha \right )} \right ] = \left [ \frac {\mu N}{\sin \left (180 \degree - \alpha \right )} \right ]
या, \quad \left ( \frac {N}{\cos \alpha} \right ) = \left ( \frac {\mu N}{\sin \alpha} \right )
या, \quad \left ( \frac {\sin \alpha}{\cos \alpha} \right ) = \left ( \frac {\mu N}{N} \right )
अतः \quad \tan \alpha = \mu
परन्तु, घर्षण गुणांक ( coefficient of friction ) की परिभाषा के अनुसार –
\mu = \tan \phi
अतः \quad \tan \alpha = \tan \phi
या, \quad \alpha = \phi
इसलिए चरम अवस्था ( limiting condition ) में, तल का झुकाव कोण ( angle of inclination ),घर्षण कोण ( angle of friction ) के ठीक बराबर होता है।
Motion down an inclined plane
झुके तल पर नींचे कि ओर गति
चित्र के अनुसार, मान लें कि झुकाव कोण को बढ़ाया जाता है और ब्लॉक को संतुलन ( equilibrium ) में रखने के लिए एक खिंचाव बल ( P ) को तल के साथ ( \theta ) के कोण पर लगाया जाता है।
अब खिंचाव बल ( P ) को उसके आयताकार घटकों ( rectangular components ) में विघटित करने पर हम पाते हैं कि –
- तल के लंबवत दिशा में खिंचाव बल का प्रभाव ( P \sin \theta ) है।
- तल के सामानांतर दिशा में खिंचाव बल का प्रभाव ( P \cos \theta ) है।
मान लें कि, खिंचाव बल ( P ) पर्याप्त न होने के कारण वस्तु तल पर नींचे कि ओर खिसकना चाहती है।

इस अवस्था में, चित्र कि ज्यामिति से हम पाते हैं कि –
( P \cos \theta + f ) = mg \sin \alpha
या \quad ( P \cos \theta + \mu \ N ) = mg \sin \alpha
और \quad ( N + P \sin \theta ) = mg \cos \alpha
या \quad N = ( mg \cos \alpha - P \sin \theta )
उपरोक्त समीकरणों से ( N ) को विस्थापित करने पर –
P \cos \theta + \mu \left (mg \cos \alpha - P \sin \theta \right ) ] = mg \sin \alpha .
या, \quad [ P \left ( \cos \theta - \mu \sin \theta \right ) ] = [ mg \left ( \sin \alpha - \mu \cos \alpha \right ) ]
या, \quad P = \left [ \frac { mg \left ( \sin \alpha - \mu \cos \alpha \right )}{ \left ( \cos \theta - \mu \sin \theta \right )} \right ]
परन्तु, \quad \mu = \tan \phi \quad
अतः \quad P = \left [ \frac {mg \left ( \sin \alpha - \tan \phi \cos \alpha \right )}{\left ( \cos \theta - \tan \phi \sin \theta \right )} \right ]
भाज्य ( numerator ) और भाजक ( denominator ) दोनों को ( \cos \phi ) से गुणा करने पर –
P = \left [ \frac {mg \left ( \sin \alpha \cos \phi - \sin \phi \cos \alpha \right )}{\left ( \cos \theta \cos \phi - \sin \phi \sin \theta \right )} \right ]
= \left [ \frac {mg \sin \left ( \alpha - \phi \right )}{\cos \left ( \theta + \phi \right )} \right ]
इस समीकरण को हल करके खिंचाव बल ( P ) के न्यूनतम मान को ज्ञात किया जा सकता है जो एक झुके तल पर वस्तु को स्थिर रखने के लिए आवश्यक होता है।
Motion up an inclined plane
झुके तल पर ऊपर कि ओर गति
अब विचार करें कि खिँचाव बल ( P ) का मान पर्याप्त होने के कारण वस्तु ऊपर कि ओर गति करने को तत्पर होती है। अतः घर्षण बल नींचे कि ओर कार्य करेगा।
इस स्थिति में वस्तु के संतुलन ( equilibrium ) के लिए –

P \cos \theta = ( f + m g \sin \alpha )
= ( \mu \ N + m g \sin \alpha )
और, \quad ( N + P \sin \theta ) = m g \cos \alpha
या, \quad N = ( m g \cos \alpha - P \sin \theta )
उपरोक्त समीकरणों से ( N ) को विस्थापित करने पर –
P \cos \theta = [ \mu \left ( m g \cos \alpha - P \sin \theta \right ) + m g \sin \alpha ]
या, \quad P \left ( \cos \theta + \mu \sin \theta \right ) = mg \left ( \sin \alpha + \mu \cos \alpha \right )
या, \quad P = \frac { m g \left ( \sin \alpha + \mu \cos \alpha \right )}{ \left ( \cos \theta + \mu \sin \theta \right )}
परन्तु \quad \mu = \tan \phi
अतः \quad P = \left [ \frac { m g \left ( \sin \alpha + \tan \phi \cos \alpha \right )}{ \left ( \cos \theta + \tan \phi \sin \theta \right )} \right ]
भाज्य ( numerator ) और भाजक ( denominator ) दोनों को ( \cos \phi ) से गुणा करने पर –
P = \left [ \frac { m g \left ( \sin \alpha \cos \phi + \sin \phi \cos \alpha \right )}{ \left ( \cos \theta \cos \phi + \sin \phi \sin \theta \right )} \right ]
= \left [ \frac {mg \sin \left ( \alpha + \phi \right )}{\cos \left ( \theta - \phi \right )} \right ]
इस अभिव्यक्ति में, बल ( P ) का मान न्यूनतम होने के लिए, भाजक ( denominator ) का मान अधिकतम या भाज्य का मान न्यूनतम होने होगा। परन्तु ( mg ), \ ( \alpha ) \ \text {और} \ ( \phi ) नियतांक ( constants ) हैं। इसलिए भाज्य ( numerator ) \left [ mg \sin ( \alpha + \phi ) \right ] भी एक नियतांक होगा।
अतः बल ( P ) का मान न्यूनतम होने के लिए, भाजक \left [ \cos ( \theta – \phi ) \right ] का मान अधिकतम होना चाहिए।
हम जानते हैं कि, ( \cos \theta ) का अधिकतम मान 1 होता है। परन्तु 1 = \cos 0 \degree
अर्थात् \quad [ ( \theta – \phi ) = 0 \degree ]
अतः \quad \theta = \phi
बल ( P ) के समीकरण में ( \theta = \phi ) का मान रखने पर –
P_{Minimum} = mg \sin \left ( \alpha + \phi \right )
इसलिए किसी वस्तु को झुके हुए तल पर ऊपर खींचने के लिए न्यूनतम बल ( least force ) का मान \left [ mg \sin ( \alpha + \phi ) \right ] होता है जब उस बल को तल से ( \theta = \phi ) के कोण में लगाया जाता है।
Motion, when force act horizontal
क्षैतिज बल के कारण गति
दिखाए गए चित्र पर विचार करें। माना कि खिंचाव बल ( P ) को क्षैतिज दिशा में लगाया जाता है।

जब वस्तु ऊपर कि ओर गति के लिए तत्पर होती है –
बलों के सामानांतर चतुर्भुज ( parallelogram law of forces ) के नियम के अनुसार –
P \cos \alpha = ( mg \sin \alpha + \mu N )
और \quad N = ( P \sin \alpha + mg \cos \alpha )
उपरोक्त समीकरणों से ( N ) को विस्थापित करने पर –
P \cos \alpha = \left [ mg \sin \alpha + \mu \left ( mg \cos \alpha + P \sin \alpha \right ) \right ]
या \quad P \left ( \cos \alpha - \mu \sin \alpha \right ) = mg \left ( \sin \alpha + \mu \cos \alpha \right )
या, \quad P = \left [ \frac {mg \left ( \sin \alpha + \mu \cos \alpha \right )}{ \left ( \cos \alpha - \mu \sin \alpha \right )} \right ]
= \left [ \frac {mg \left ( \sin \alpha + \tan \phi \cos \alpha \right )}{ \left ( \cos \alpha - \tan \phi \sin \alpha \right )} \right ]
भाज्य ( numerator ) और भाजक ( denominator ) दोनों को ( \cos \phi ) से गुणा करने पर –
P = \left [ \frac {mg \left ( \sin \alpha \cos \phi + \sin \phi \cos \alpha \right )}{ \left ( \cos \alpha \cos \phi - \sin \phi \sin \alpha \right )} \right ]
= \left [ \frac {mg \sin \left ( \alpha + \phi \right )}{ \cos \left ( \alpha + \phi \right )} \right ] = \left [ mg \tan \left ( \alpha + \phi \right ) \right ]
जब वस्तु नींचे कि ओर गति के लिए तत्पर होती है, तब –
P \cos \alpha = ( mg \sin \alpha - \mu N )
और, \quad N = ( P \sin \alpha + mg \cos \alpha )
उपरोक्त समीकरणों को ऊपर वर्णित विधि द्वारा हल करने से हम पाते हैं कि –
P = \left [ mg \tan \left ( \alpha - \phi \right ) \right ]
अतः इस समीकरण से यह निष्कर्ष निकलता है कि –
- जब ( \alpha > \phi ) (अर्थात् झुकाव कोण का मान, घर्षण कोण से अधिक होता है ) तब वस्तु, तल पर स्वयं फिसलने लगती है और बल ( P ) का मान घनात्मक होता है। अर्थात् वस्तु को तल पर स्थिर रखने के लिये [mg \tan ( \alpha + \phi ) ] मान के एक बल को चित्र में दिखाए गए दिशा में लगाने कि आवश्यकता पड़ती है।
- जब ( \alpha < \phi ) (अर्थात् झुकाव कोण का मान, घर्षण कोण से कम होता है ) तब वस्तु तल पर स्थिर होती है और बल ( P ) का मान ऋणात्मक होता है।अर्थात् वस्तु को तल पर नींचे कि ओर खिसकने के लिये [mg \tan ( \alpha - \phi ) ] मान के एक बल को चित्र में दिखाए गए दिशा के विपरीत दिशा में लगाए जाने की आवश्यकता पड़ती है।