What is Machine Efficiency?
मशीन दक्षता क्या है?
किसी मशीन ( machine ) की दक्षता ( efficiency ) को, मशीन के द्वारा प्राप्त कार्य ( output work ) और मशीन पर किए गए कार्य ( input work ) के अनुपात के रूप में परिभाषित किया जाता है।
इसलिए, \quad \text {Efficiency} ( \eta ) = \left ( \frac{\text {आउटपुट कार्य }}{\text {इनपुट कार्य}} \right )
उदहारण के लिए, चित्र में दिखाए गए एक उत्तोलक ( lever ) के कार्य पर विचार करें।
मान लीजिए कि, उत्तोलक पर एक प्रयास बल ( effort ) ( P ) को ( T ) समय के लिए लगाया जाता है। इतने समय में प्रयास बिंदु ( effort point ) ( A ) दूरी ( x ) तक गमन करती है और लोड पॉइंट ( load point ) ( B ) दूरी ( y ) तक गमन करती है।
कार्य ( work ) की परिभाषा के अनुसार –
कार्य \quad = \text {बल} \ \times \ \text {दुरी}
अतः मशीन का इनपुट कार्य ( P \times x ) है और आउटपुट कार्य ( W \times y ) है।
घर्षण बल ( frictional force ) की अनुपस्थिति में, ऊर्जा संरक्षण सिद्धांत ( conservation of energy ) से –
( P \times x ) = ( W \times y )
या, \quad \left ( \frac {W}{P} \right ) = \left ( \frac {x}{y} \right )
परन्तु, \left ( \frac {W}{P} \right ) को मशीन का यांत्रिक लाभ ( Mechanical Advantage ) है और \left ( \frac {x}{y} \right ) मशीन का वेलॉसिटी रेसिओ ( Velocity Ratio ) है।
अतः घर्षण बल की अनुपस्थिति में, एक आदर्श मशीन ( ideal machine ) के लिए –
\text {Mechanical advantage (यांत्रिक लाभ)} = \text {Velocity Ratio (वेलॉसिटी रेसिओ)}
परन्तु, वास्तविक परिस्थितियों में सभी मशीनों में घर्षण होता है। इस घर्षण के कारण इनपुट कार्य की कुछ मात्रा क्षय होता है जो ताप ( heat energy ) में परिवर्तित होकर मशीन के पुर्जों के टूटने-फूटने ( wear and tear ) का कारण बनता है।
इसलिए, मशीनों में आउटपुट कार्य, इनपुट कार्य से हमेशा कम होता है और इसके कारण मशीन के प्रदर्शन में कमी आती है। अतः किसी मशीन के प्रदर्शन ( performance ) को दर्शाने के लिए, दक्षता ( efficiency ) शब्द का प्रयोग किया जाता है।
अतः मशीनों के पुर्जो में घर्षण की उपस्थिति से मशीन की दक्षता ( machine efficiency ) की अवधारणा को जन्म हुआ है।
दक्षता ( efficiency ) यह बताती है कि – ” कोई मशीन, इनपुट ऊर्जा में न्यूनतम नुकसान के साथ घर्षण बलों को दूर करने में कितनी सक्षम है?”

Magnitude of efficiency
दक्षता का परिमाण
किसी मशीन की दक्षता इस प्रकार व्यक्त की जाती है –
\eta = \left ( \frac{\text {आउटपुट कार्य }}{\text {इनपुट कार्य}} \right ) = \left ( \frac {Wy}{Px} \right )
= \left ( \frac {W}{P} \right ) \times \left ( \frac {y}{x} \right )
= \left ( \frac {\text {Mechanical Advantage}}{\text {Velocity Ratio}} \right )
इसलिए, मशीन की दक्षता को यांत्रिक लाभ ( MA ) और वेलोसिटी रेसिओ ( VR ) के अनुपात के रूप में भी परिभाषित किया जाता है।
एक आदर्श मशीन ( ideal machine ) के लिए –
\text {Mechanical Advantage} = \text {Velocity Ratio}
अतः एक आदर्श मशीन का \quad \eta = 1 होता है।
मशीन का वेलॉसिटी रेसिओ, मशीन की डिज़ाइन पर आधारित आयामी पैरामीटर ( dimensional parameter ) होता है और यह केवल पुर्जो की ज्यामिति पर निर्भर करता है। यही कारण है कि वेलॉसिटी रेसिओ ( velocity ratio ), घर्षण के किसी भी प्रभाव से स्वतंत्र होता है।
Ideal effort & Actual effort
आदर्श प्रयास और वास्तविक प्रयास
हम जानते है कि, दक्षता ( efficiency ) इस प्रकार होती है –
\eta = \left ( \frac {Wy}{Px} \right )
अतः \quad P = \left ( \frac { Wy }{ x \eta } \right )
परन्तु, आदर्श मशीन दक्षता ( ideal machine efficiency ) इस प्रकार होती है –
\eta_{Ideal} = 1
अतः \quad P_{Ideal} = \left ( \frac { Wy }{ x } \right )
मान लें कि, ( W ) कार्य को करने के लिए आवश्यक actual effort का परिमाण ( P_{Actual} ) है।
अतः \quad P_{Actual} = \left ( \frac { Wy }{ x \eta} \right )
इसलिए, आदर्श प्रयास ( ideal effort ) और वास्तविक प्रयास ( actual effort ) का सम्बन्ध इस प्रकार होगा –
\left ( \frac {P_{Actual}}{P_{Ideal}} \right ) = \left ( \frac { Wy }{ x \eta} \right ) \div \left ( \frac { Wy }{ x } \right )
या, \quad \left ( \frac {P_{Actual}}{P_{Ideal}} \right ) = \left ( \frac {1}{\eta} \right )
अतः मशीन की दक्षता ( machine efficiency ) को इस प्रकार भी दर्शाया जा सकता है –
\eta = \left ( \frac{\text {आदर्श प्रयास}}{\text {वास्तविक प्रयास}} \right )
= \left ( \frac { P_{Ideal}}{ P_{Actual}} \right )
Law of machine
मशीन का नियम
प्रयोगों से प्राप्त, वास्तविक प्रयास ( actual effort ) ( P_{Actual} ) , भार ( load ) ( W ) और घर्षण ( friction ) ( C ) के बीच एक संबंध प्राप्त किया जा सकता है। यह संबंध को इस प्रकार समीकरण से व्यक्त किया जाता है –
P_{Actual} = m W + C
इस समीकरण को मशीन का नियम ( Law of a Machine ) कहा जाता है।

प्रयोग द्वारा प्राप्त परिणामों को चित्र में दिखाए गए एक आलेख ( graph ) में दर्शाया जा सकता है। इसके लिए मशीन पर, वास्तविक प्रयास ( actual effort ) के विभिन्न मान को Y अक्ष पर और लोड संबंधित मान को X अक्ष पर आलेखित किया जाता है।
इस आलेख को, लोड – वास्तविक प्रयास आलेख ( Load – Actual effort Graph ) के नाम से जाना जाता है।
एक आदर्श मशीन के लिए, भार और वास्तविक प्रयास ( load-actual effort ) का आलेख एक सरल रेखा होती है जो मूल बिंदु से होकर गुजरती है। परन्तु, एक वास्तविक मशीन के लिए यह सरल रेखा, Y अक्ष को घनात्मक दिशा में काटते हुए गुजरती है।
समीकरण में C का मान, मशीन पर कोई लोड न होने पर घर्षण का मुकाबला करने के लिए आवश्यक प्रयास को इंगित करता है। यह शुन्य लोड पर मशीन को चलाने या शुरू करने के लिए आवश्यक प्रयास की मात्रा है।
आलेख का ढलान ( slope ) इस प्रकार होगा –
m = \tan \theta
आलेख कि ज्यामिति से हम पाते हैं कि –
\tan \theta = \left ( \frac {P_{Ideal}}{W} \right )
अतः \quad P_{Ideal} = m W
परन्तु, यांत्रिक लाभ ( mechanical advantage ) \quad MA = \left ( \frac {W}{P_{Ideal}} \right ) = \left ( \frac {W}{mW} \right ) = \left ( \frac {1}{m} \right )
अतः \quad \tan \theta = \left ( \frac {1}{MA} \right )
इसलिए, मशीन के समीकरण को इस प्रकार भी लिखा जा सकता है –
P_{Actual} = P_{Ideal} + C
= m W + C
Graph of load & ideal effort
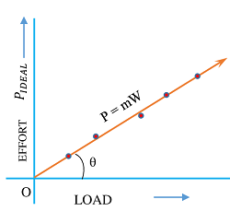
लोड – आदर्श प्रयास आलेख
लोड ( W ) और प्रयास ( P_{Ideal} ) के बीच के संबंध को प्राप्त करने के लिए हम एक आलेख प्लॉट कर सकते हैं।
इसके लिए, मशीन पर विभिन्न मान के लोड और प्रयास के संगत मान को सूचीबद्ध किया जाता है। लोड के मान को X अक्ष और प्रयास ( P_{Ideal} ) को Y अक्ष पर प्लॉट किए जाता है।
आदर्श परिस्थितियों में घर्षण को नगण्य माना जाता है। इस प्रकार ( C ) का मान शून्य हो जाता है।
इसलिए, भार और आदर्श प्रयास ( load-ideal effort ) का आलेख, एक सरल रेखा होती है जो मूल बिंदु से होकर गुजरती है।
अतः इस रेखा का समीकरण इस प्रकार होगा –
P_{Actual} = m W
यहाँ, स्थिर पद ( C ) शून्य हो जाता है क्योंकि घर्षण शुन्य होता है।
Graph of load & mechanical advantage

लोड – यांत्रिक लाभ आलेख
लोड और यांत्रिक लाभ के बीच संबंध प्राप्त करने के लिए, मशीन पर लोड के विभिन्न मान और MA के संबंधित मान को सूचीबद्ध किया जाता है। लोड के मान को X अक्ष और यांत्रिक लाभ के मान को Y अक्ष पर प्लॉट किया जाता है।
भार और यांत्रिक लाभ ( Load-mechanical advantage ) का आलेख, एक वक्र रेखा है जैसा की चित्र में दिखाया गया है।
आलेख से स्पष्ट है कि, जैसे-जैसे लोड बढ़ता है, यांत्रिक लाभ भी बढ़ता जाता है। परन्तु, घर्षण के कारण यांत्रिक लाभ में वृद्धि की दर, लोड में वृद्धि की दर से कम होती है। इसलिए वक्र अधिक लोड पर आधार की ओर झुकता जाता है।
मशीन के नियम ( law of a machine ) कि अभिव्यक्ति में ( C ) एक नियतांक पद है। इसलिए, जब \left ( \frac {W}{P} \right ) का अनुपात कम होता है तब C का प्रभाव अधिक होता है।
अनुपात \left ( \frac {W}{P} \right ) के उच्च मान पर C का प्रभाव धीरे-धीरे कम होकर अंततः नगण्य हो जाता है। अतः वक्र चपटा होकर X अक्ष के लगभग समानांतर हो जाता है।
Graph of load & efficiency
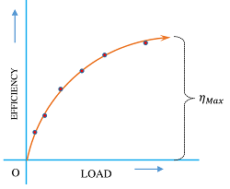
लोड – दक्षता आलेख
लोड और प्रतिशत दक्षता के बीच आलेख के लिए मशीन पर विभिन्न मान के लोड और दक्षता से संबंधित मान को सूचीबद्ध किया जाता है। लोड के मान को X अक्ष और प्रतिशत दक्षता को Y अक्ष पर प्लॉट किया जाता है।
भार और प्रतिशत दक्षता ( Load-percentage efficiency ) का आलेख, एक वक्र रेखा होता है जैसा कि चित्र में दिखाया गया है।
Velocity ratio, डिज़ाइन पर आधारित एक आयामी पैरामीटर ( dimensional parameter ) होता है और मशीन पुर्जों की ज्यामिति पर निर्भर करता है। इसलिए लोड में परिवर्तन होने पर भी यह स्थिर ( constant ) रहता है। परन्तु यांत्रिक लाभ, लोड पर निर्भर करता है और लोड में वृद्धि के साथ बढ़ता है।
यांत्रिक लाभ में वृद्धि के कारण, प्रतिशत दक्षता भी बढ़ जाती है। परन्तु, दक्षता में वृद्धि की दर, लोड में वृद्धि की दर से कम होता है। इसलिए वक्र झुकता जाता है और अंततः अत्यधिक लोड पर यह X अक्ष के लगभग समानांतर हो जाता है।
